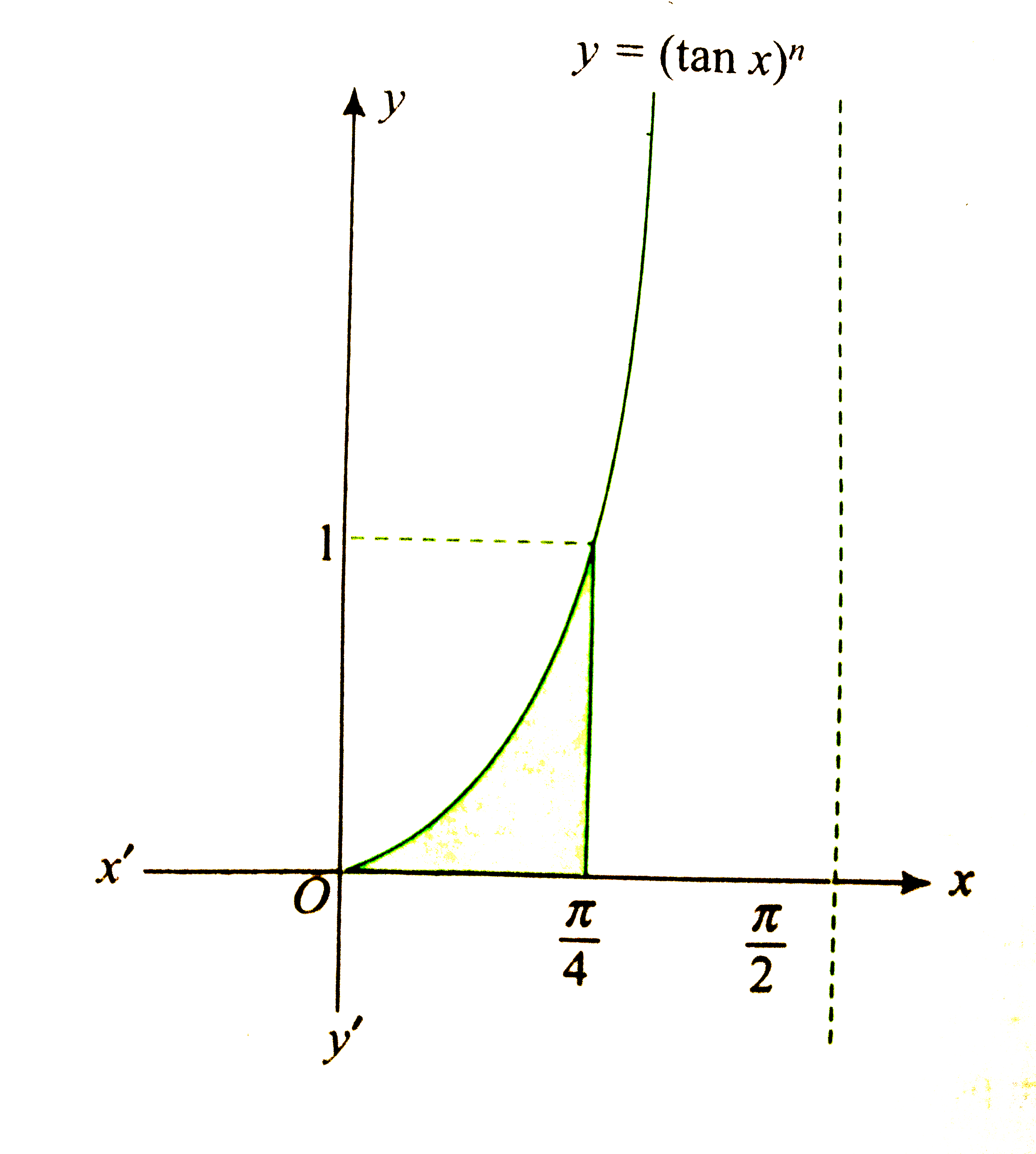
Let $A_{n}$ be the area bounded by the curve $y = {(tan x)}^{n}$ and the lines $x = 0, y = 0,$ and $x = \frac{π}{4} .$ Prove that for $n > 2, A_{n} + A_{n - 2} = \frac{1}{n - 1}$ and deduce $\frac{1}{2 n + 2} < A_{n} < \frac{1}{2 n - 2}$

Video Solution

Text Solution

Verified by Experts

$We have A_{n} = \int_{0}^{π / 4} {(tan x)}^{n} d x$

$Since 0 < t n a x < 1, when 0 < x < π / 4,$ we have
$0 < {(tan x)}^{n + 1} < {(tan x)}^{n} for each n \in N$
$\Rightarrow \int_{0}^{π / 4} {(tan x)}^{n + 1} d x < \int_{0}^{π / 4} {(tan x)}^{n} d x$
$\Rightarrow A_{n + 1} < A_{n}$
$Now, for n > 2$ ,
$A_{n} + A_{n + 2} = \int_{0}^{π / 4} [{(tan x)}^{n} + {(tan x)}^{n + 2}] d x$
$= \int_{0}^{π / 4} {(tan x)}^{n} (1 + {tan}^{2} x) d x$
$= \int_{0}^{π / 4} {(tan x)}^{n} ({sec}^{2} x) d x$
$= {[\frac{1}{(n + 1)} {(tan x)}^{n + 1}]}_{0}^{n + 1}$
$[∵ \int {[f (x)]}^{n} f' (x) d x = \frac{{[f (x)]}^{n + 1}}{n + 1}]$
$= \frac{1}{(n + 1)} (1 - 0)$
$Since A_{n + 2} < A_{n + 1} < A_{n},$ we get
$A_{n} + A_{n + 2} < 2 A_{n}$
$\Rightarrow \frac{1}{n + 1} < 2 A_{n} \Rightarrow \frac{1}{2 n + 2} < A_{n} (1)$
$Also for n > 2, A_{n} + A_{n} < A_{n} + A_{n - 2} = \frac{1}{n - 1}$
$or 2 A_{n} < \frac{1}{n - 1}$
$or A_{n} < \frac{1}{2 n - 2} (2)$
$Combining (1) and (2), we get \frac{1}{2 n + 2} < A_{n} < \frac{1}{2 n - 2} .$

Updated on:21/07/2023