Find the area bounded by the curve $f (x) = x + sin x and$ its inverse function between the ordinates $x = 0 to x = 2 π$ .

Video Solution

Text Solution

Verified by Experts

$y = x + sin x$
$∴ \frac{d y}{d x} = 1 + o s x \geq 0 \forall x$
$Also \frac{d^{2} y}{{d x}^{2}} = - sin x = 0 when x = n π, n \in Z$
Hence $x = n π$ are points of inflection, where curve changes its concavity.
$Also, for x \in (0, π), sin x > 0 \Rightarrow x + sin x > x$
$And for x \in (π, 2 π), sin x < 0 \Rightarrow x + sin x < x$
Thus, we have following graphs of function y=f(x) and its inverse function.

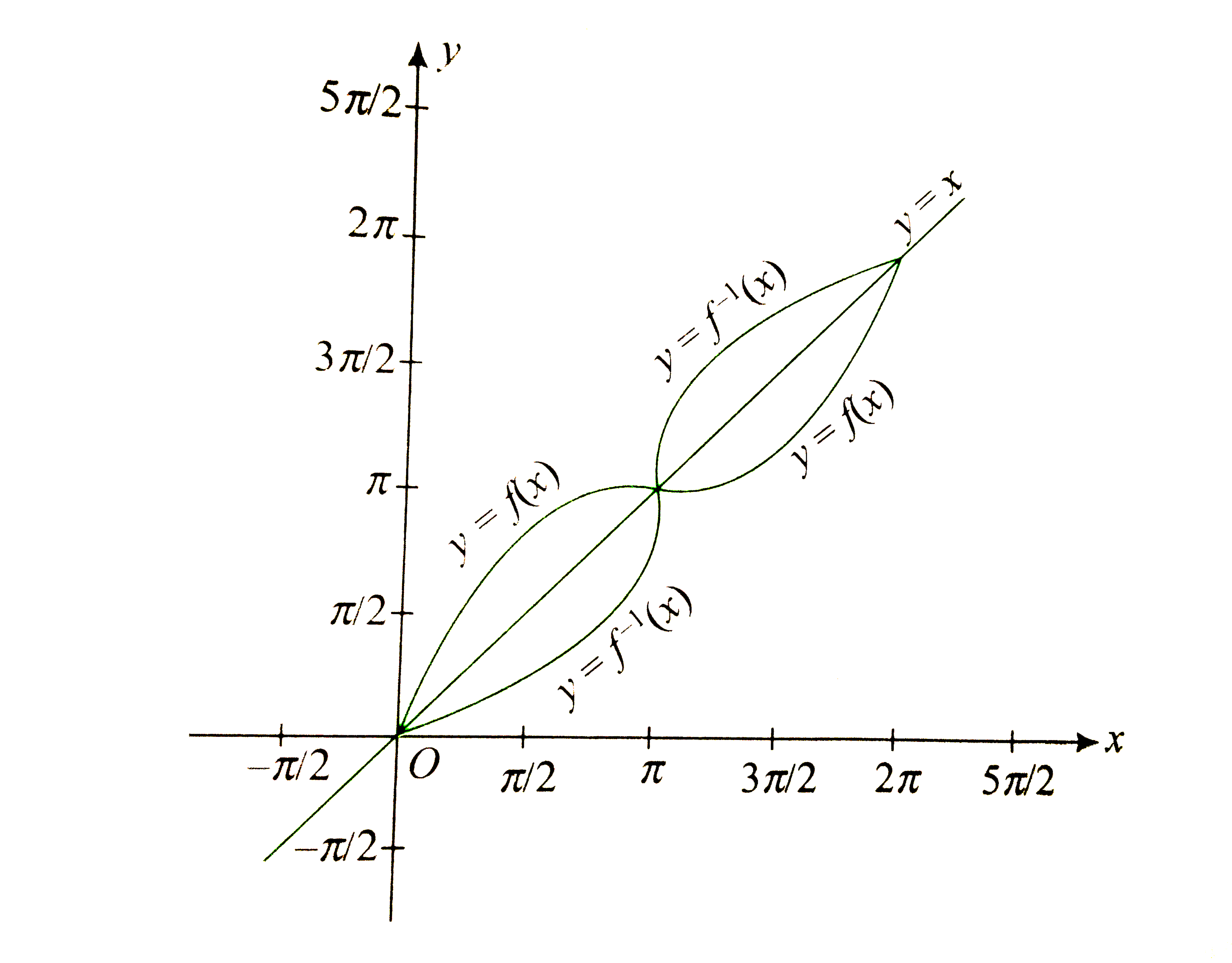
$Required area = 4 \int_{0}^{π} (f (x) - x) d x$
$= 4 \int_{0}^{π} sin x d x = 4 \times 2 = 8$ sq. units.

Updated on:21/07/2023