Find the area of the region enclosed by $y = - 5 x - x^{2} and y = x$ on interval $[- 1, 5]$

Video Solution

Text Solution

Verified by Experts

Solving the given curves we get
$5 x - x^{2} = x$
$∴ x^{2} - 4 x = 0$
$\Rightarrow x = 0, 4$
$y = x (5 - x)$ is parabola which is concave downward and intersecting x-axis at x=0 and x=5.

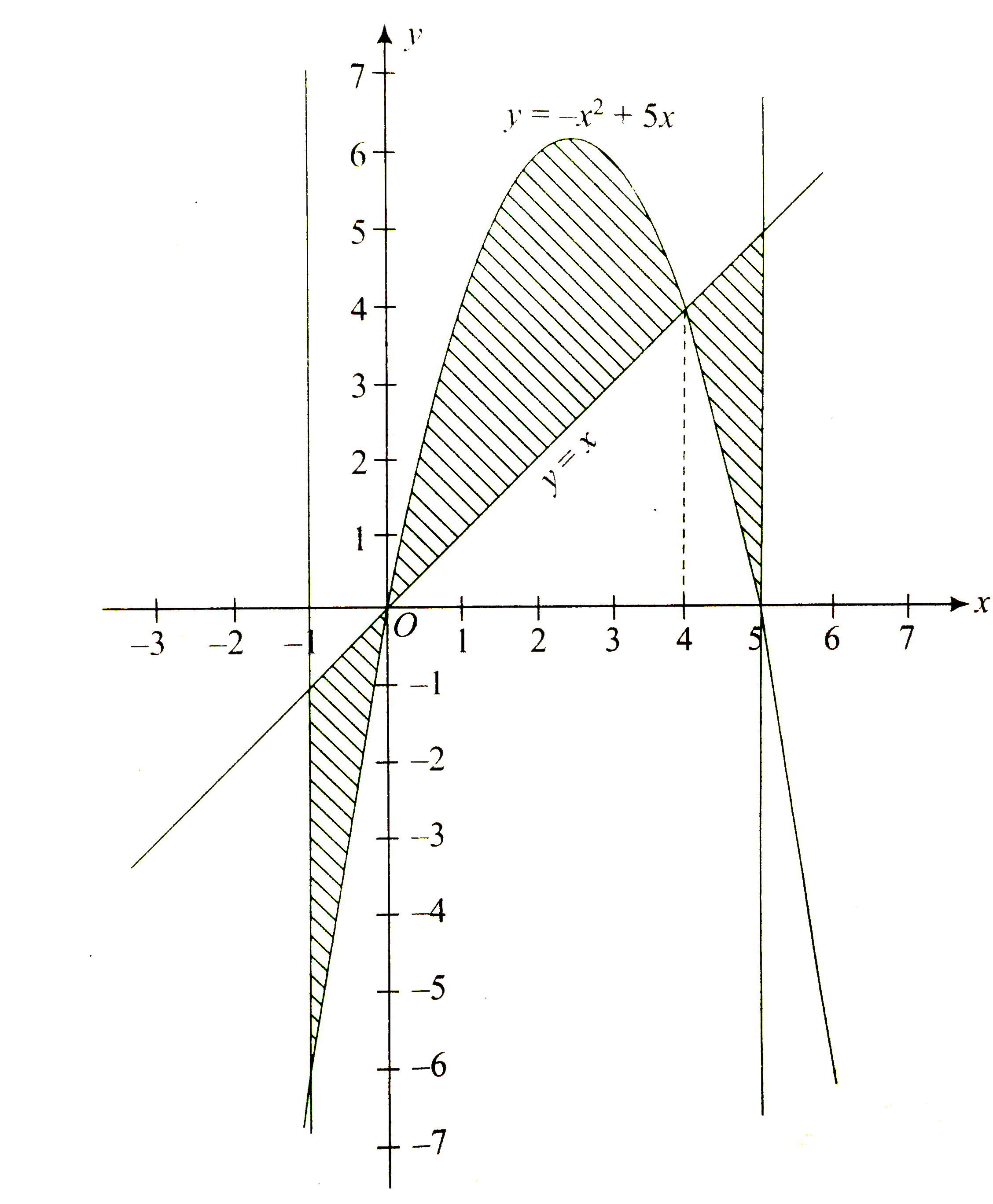
$Required area, = 5 \int - 1 ∣ ∣ x - (5 x - x^{2}) ∣ ∣ d x$
$= 5 \int - 1 | x - 4 x | d x$
$= 0 \int - 1 (x^{2} - 4 x) d x + 4 \int 0 (4 x - x^{2}) d x + 5 \int 4 (x^{2} - 4 x) d x$
$= {[\frac{x^{3}}{3} - 2 x^{2}]}_{- 1}^{2} + {[2 x^{2} - \frac{x^{3}}{3}]}_{0}^{2} + [\frac{x^{3}}{3} - 2 x^{2}]$
$= - [\frac{- 1}{3} - 2] + [32 - \frac{64}{3}] + [\frac{125}{3} - 50] - [\frac{64}{3} - 32]$
$= 16 - \frac{2}{3}$
$\frac{46}{3}$ sq. units.

Updated on:21/07/2023

The area of the region enclosed by $y = x^{3} - 2 x^{2} + 2 and y = 3 x + 2$ is
A $\frac{71}{6}$
B14
C $\frac{29}{3}$
D $\frac{71}{3}$
What are the area of the region enclosed by $y = 2 | x |$ and $y = 4$ ?
A2 sq. units
B4 sq.units
C8 sq. units
D16 sq. units
What is the area of the region enclosed by $y = 2 | x |$ and $y = 4$ ?
A2 square unit
B $4$ square unit
C8 square unit
D16 squre unit