Consider the region formed by the lines x=0,y=0,x=2,y=2. If the area enclosed by the curves y=exandy=1nx, within this region, is being removed, then find the area of the remaining region.
Video Solution
Text Solution
y=exandy=logex are inverse to each other.
So, their graphs are symmetrical about the line y=x.
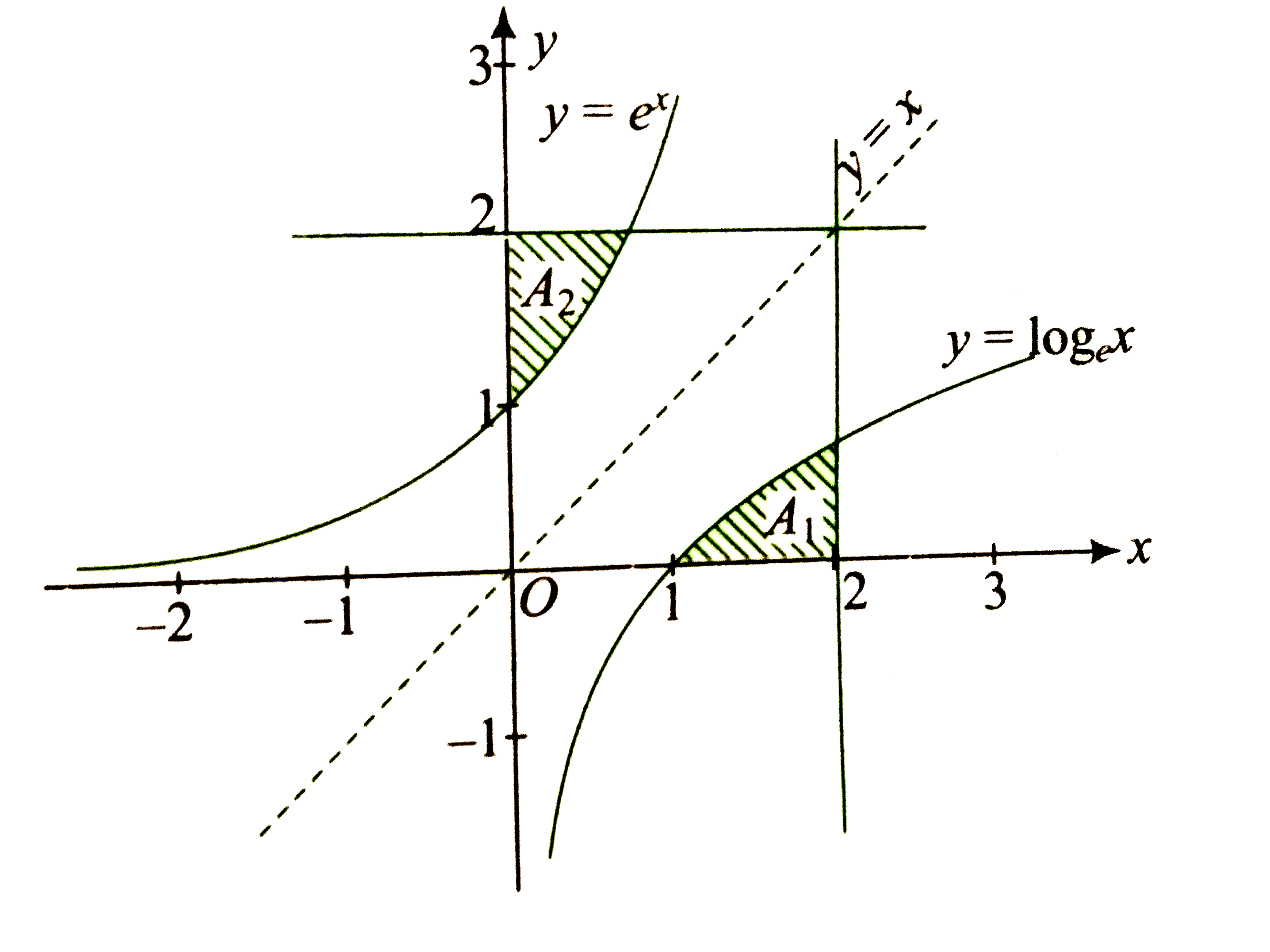
Area of the square OABC is 4 sq. units.
Areas A1andA2 are same.
So, area of the shaded region =2A1
=22∫1logexdx
=2[xlogex−x]21
=2[2loge2−1] sq. unit
Therefore, the area of the unshaded region of the square
=4−2[2loge2−1]=(6−4loge2) sq. units
|
Topper's Solved these Questions
- AREABook:CENGAGEChapter:AREAExercise:Exercise 9.1
Explore 9 Videos
- AREABook:CENGAGEChapter:AREAExercise:Exercise 9.2
Explore 14 Videos
- APPLICATIONS OF DERIVATIVESBook:CENGAGEChapter:APPLICATIONS OF DERIVATIVESExercise:Question Bank
Explore 29 Videos
- AREA UNDER CURVESBook:CENGAGEChapter:AREA UNDER CURVESExercise:Question Bank
Explore 20 Videos
Similar Questions
Knowledge Check
The area of the region enclosed by the curves y=x,x=e,y=1x and the positive x-axis is
A52 square unitsB12 square unitsC1 square unitsD32 square unitsThe area enclosed by the region y22≤x≤y+4 is
A16B8C18D12The area (in sq unit) of the region enclosed by the curves y=x2andy=x3 is
A112B16C13D1
The area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionIndicate the region bounded by the curves y=x2,y=x+2 and x-axis and obtain the area enclosed by them
View SolutionThe area of the region bounded by the curve y=ex and lines x=0 and y=e is
View SolutionArea of the region bounded by the curve y=ex and lines x = 0 and y = e is :
View SolutionArea of the region enclosed between the curve x=1−y2 and the Y-axis is
View Solution
