Let $f (x) =$ maximum ${x^{2}, {(1 - x)}^{2}, 2 x (1 - x)}$ where $x \in [0, 1] .$ Determine the area of the region bounded by the curve $y = f (x)$ and the lines $y = 0, x = 0, x = 1 .$

Video Solution

Text Solution

Verified by Experts

$f (x) = Maximum {x^{2}, (1 - x^{2}), 2 x (1 - x)}$
We draw the graphs of
$y = x^{2} (1)$
$y = (1 - x^{2}) (2)$
$y = 2 x (1 - x) (3)$
Solving (1) and (3), we get $x^{2} = 2 x (1 - x)$
$or 3 x^{2} = 2 x \Rightarrow x = 0 or x = 2 / 3 .$
Solving (2) and (3) we get ${(1 - x)}^{2} = 2 x (1 - x)$
$\Rightarrow x = 1 / 3 and x = 1,$

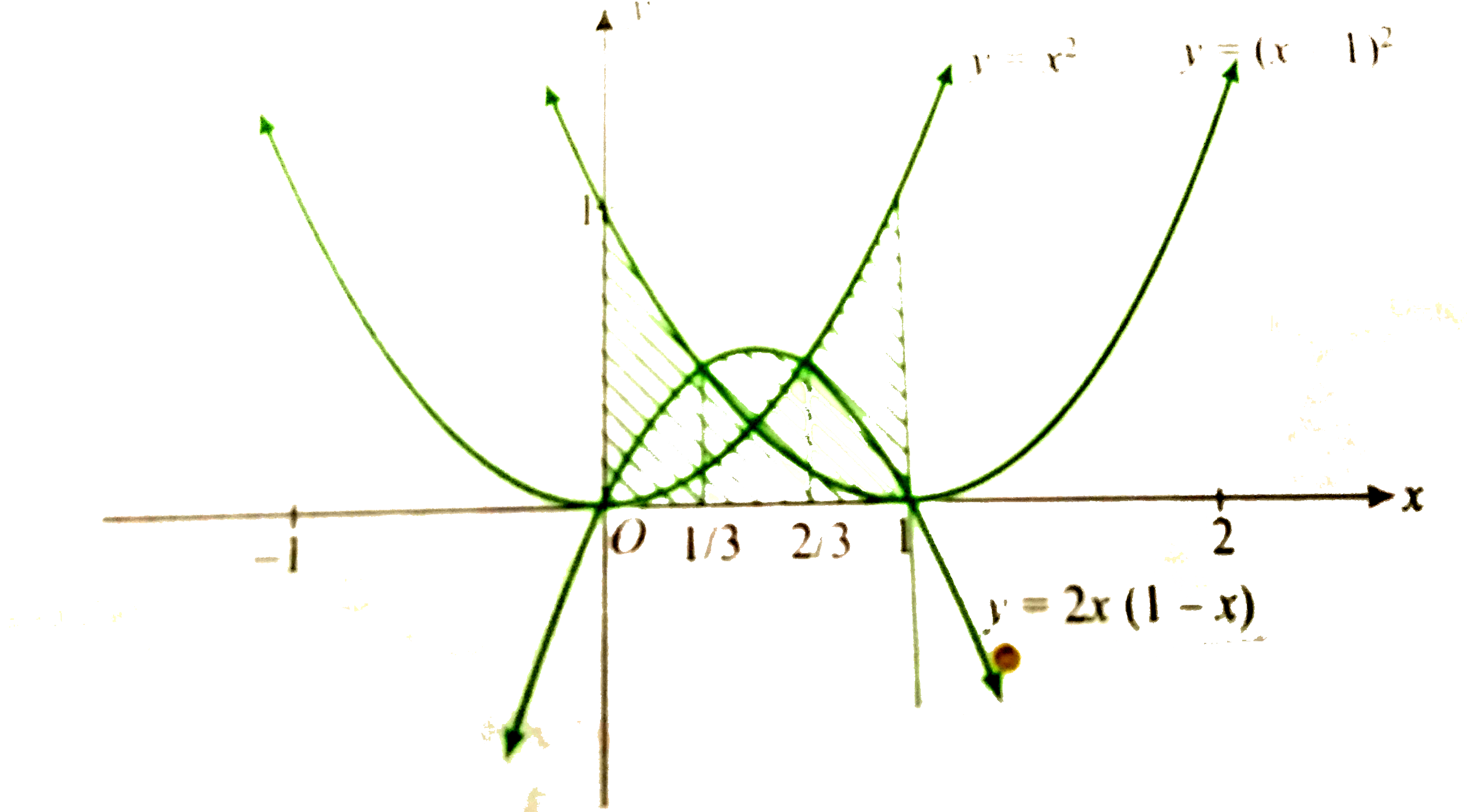
From the figure, it is clear that
$f (x) ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ \begin{matrix} (1 - x^{2}) & for & 0 \leq x \leq 1 / 3 2 x (1 - x) & for & 1 / 3 \leq x \leq 2 / 3 x^{2} & for & 2 / 3 < x \leq 1 \end{matrix}$
The required area A is given by
$A = \int_{0}^{1} f (x) d x$
$= f_{0}^{1 / 3} {(1 - x)}^{2} d x + f_{1 / 3}^{2 / 3} 2 x (1 - x) d x + \int_{2 / 3}^{1} x^{2} d x$
$= - {[\frac{1}{3} {(1 - x)}^{3}]}_{0}^{3} + {[(x^{2} - \frac{2 x^{3}}{3})]}_{1 / 3}^{2 / 3} + {[\frac{x^{3}}{3}]}_{2 / 3}^{1}$
$= - \frac{1}{3} {(\frac{2}{3})}^{3} + \frac{1}{3} + {(\frac{2}{3})}^{2} - \frac{2}{3} {(\frac{2}{3})}^{3} - {(\frac{1}{3})}^{2} + \frac{2}{3} {(\frac{1}{3})}^{3} + \frac{1}{3} - \frac{1}{3} {(\frac{2}{3})}^{3}$
$= \frac{17}{27}$ sq. units.

Updated on:21/07/2023

The area of the region bounded by the curve C $: y = \frac{x + 1}{x^{2} + 1}$ nad the line y=1 , is
Aml $- \frac{1}{2} In 2 + \frac{π}{4}$
B $In 2 - \frac{π}{4} + 1$
C $\frac{1}{2} In 2 + \frac{π}{4} - 1$
DIn $2 - \frac{π}{2} + 1$
The area of the region bounded by the curves $y^{2} = 4 a^{2} (x - 1)$ and the lines x = 1 and y = 4a, is
A $\frac{21 a}{2}$ sq unit
B $\frac{16}{3}$ sq unit
C $\frac{17 a}{3}$ sq unit
D $\frac{16 a}{3}$ sq unit
Find the area of the region bounded by the curve $y = | x + 1 |$ , lines $x = - 4, x = 2$ and X-axis.
A $5$
B $7$
C $6$
D $9$