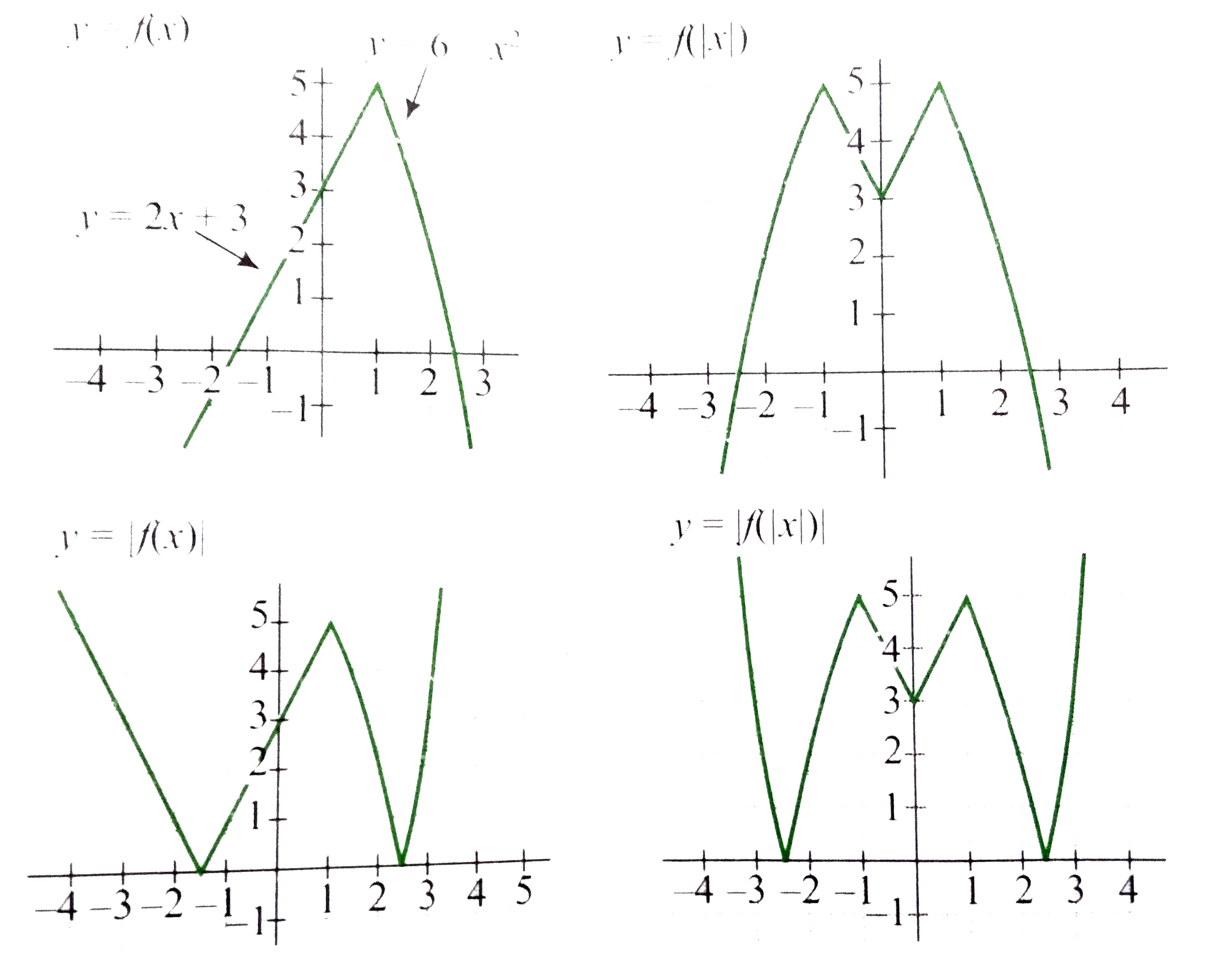Consider the function f(x)={2x+3,x≤1and−x2+6,x>1 Then draw the graph of the function y=f(x),y=f(|x|),y=|f(x)|,andy=|f(x)|.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.115videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.25videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank31videos
Quadratic Equations, Inequalities, Modulus and Logarithms
- BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
Similar Questions
Consider the function f(x)={2x+3,x≤1and−x2+6,x>1 Then draw the graph of the function y=f(x),y=f(|x|),y=|f(x)|,andy=|f(x)|.
View SolutionConstruct the graph of the function y=f(x−1)+f(x+1) where f(x)=1−|x| where |x|≤1, f(x)=0 where |x|>1
View SolutionDraw the graph of the function y=f(x)=tan−1(1−x21+x2).
View SolutionIf f(x)=sin(πx), then draw the graph of the followings : (i) y=f(|x|) (ii) y=f(−|x|) (iii) |y|=f(x)
View SolutionDraw the graph of:
y=f(x)=3sin(2x−1).View SolutionGiven the graph of y=f(x).
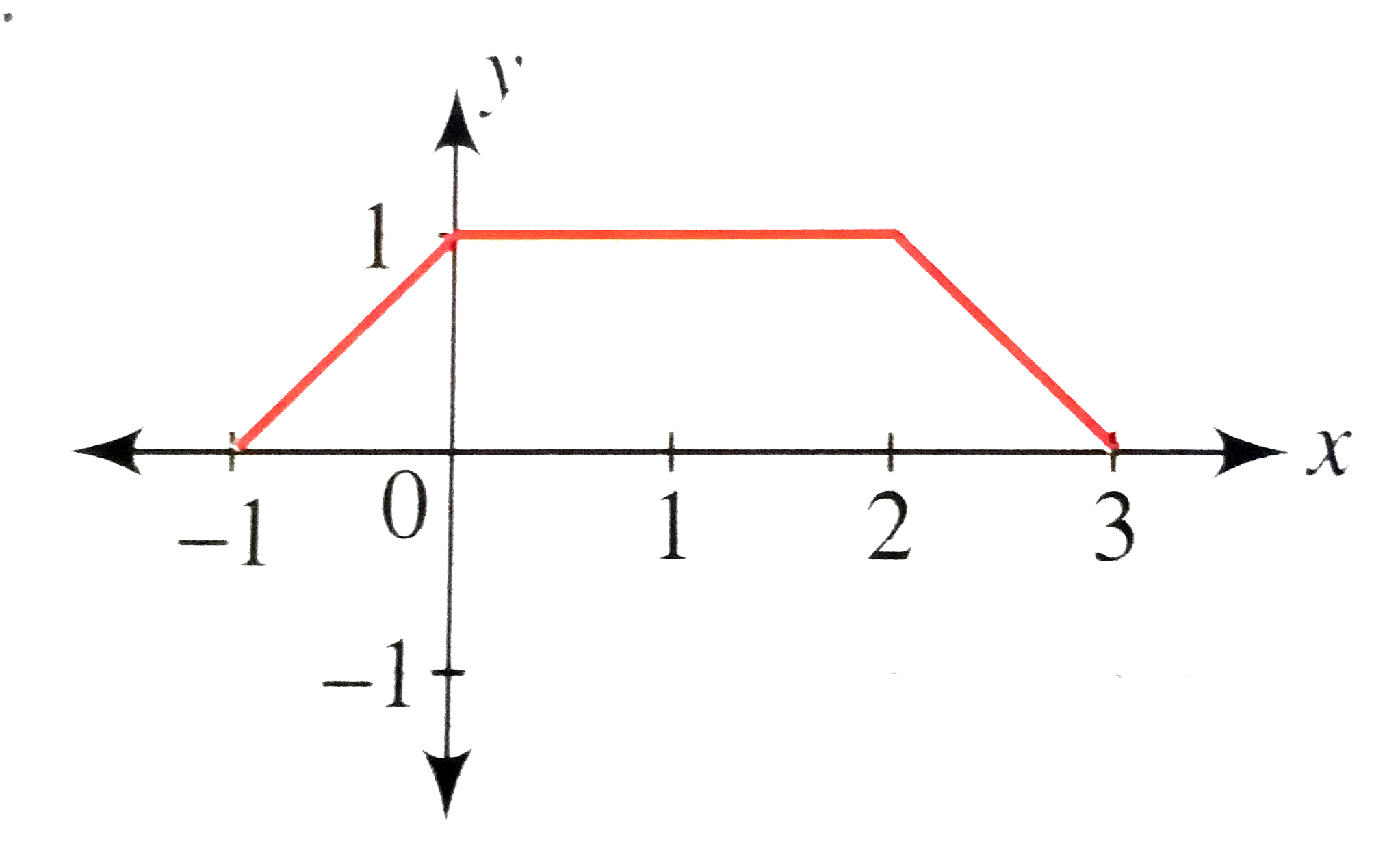
Draw the graphs of the followin.
(a) y=f(1−x) (b) y=−2f(x)
(c) y=f(2x) (d) y=1−f(x)View SolutionThe graph of the function y=f(x) is as shown in the figure.
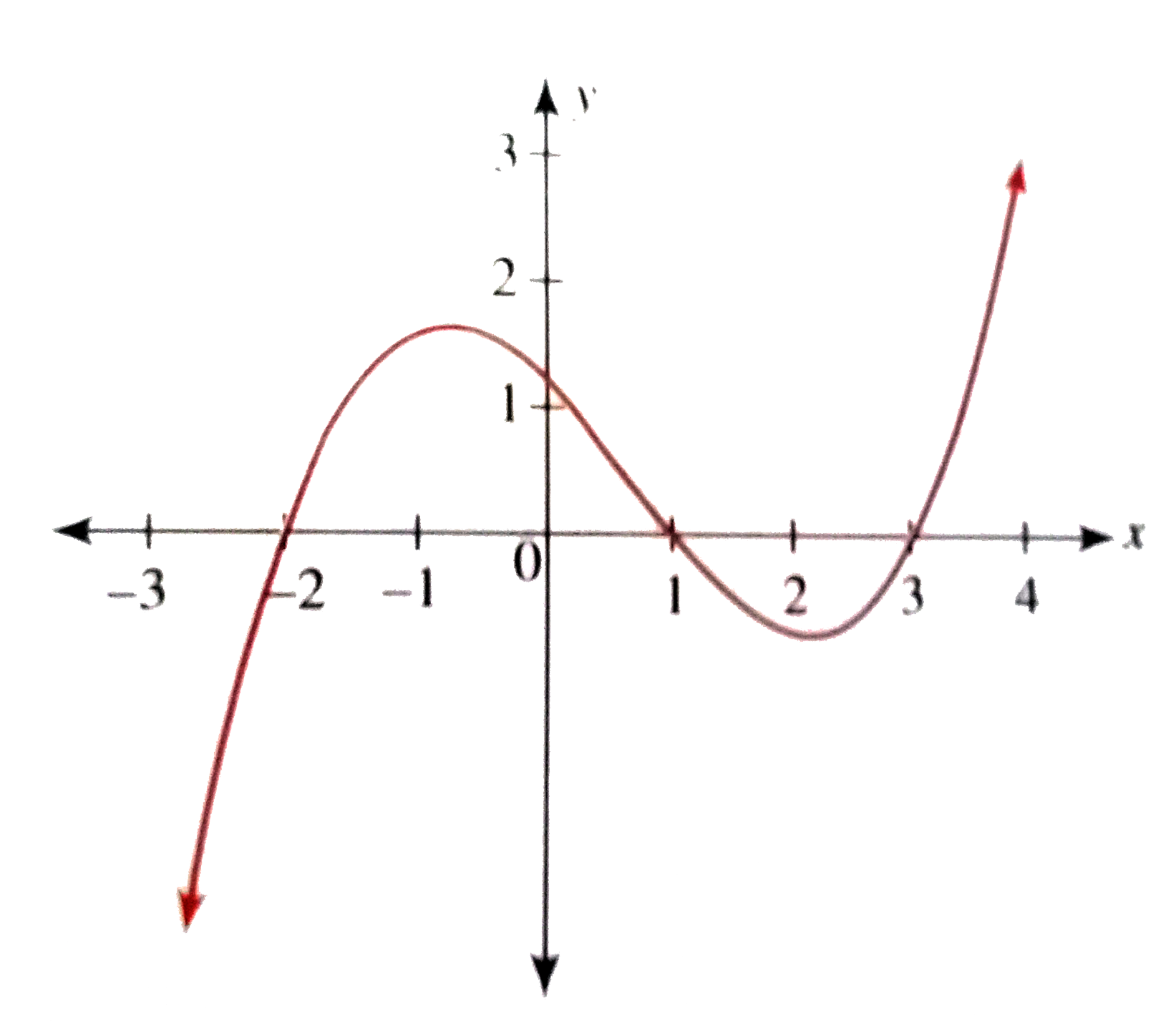
Then draw the graphs of
(i) |y|=sgn(f(x)) (ii) |y|=|f(x∣)|
(iii) y=xsgn(f(x))View SolutionDraw the graph of y=f(x)=x+1x2+1
View SolutionDraw the graph of y=f(x)=x2x2+1.
View SolutionIf the graph of the function y=f(x) is as shown : the graph of y=12(|f(x)|−f(x)) is
View Solution