A liquid in a beaker has temperature ϕ(t) at time t and θ0 is temperature of surroundings, then according to Newton's law of cooling the correct graph between loge(θ−θ0) and t is Solution in Kannada


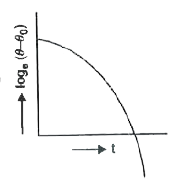

The correct Answer is:B
dθdt=−K(θ−θ0)
∫θθ0dθθ−θ0=−K∫t0dt
lnθ0−θ0=−Kt+C
The above equation shows that graph is a straight line Correct choice is (b).
Topper's Solved these Questions
- TRANSFERENCE OF HEAT Book:MODERN PUBLICATIONChapter:TRANSFERENCE OF HEAT Exercise:Recent Competitive Questions
Explore 4 Videos
- TRANSFERENCE OF HEAT Book:MODERN PUBLICATIONChapter:TRANSFERENCE OF HEAT Exercise:Multiple Choice Questions (Level - II)
Explore 49 Videos
- SOLIDS & SEMICONDUCTOR DEVICESBook:MODERN PUBLICATIONChapter:SOLIDS & SEMICONDUCTOR DEVICESExercise:Revision Test
Explore 28 Videos
- UNIFORM CIRCULAR MOTIONBook:MODERN PUBLICATIONChapter:UNIFORM CIRCULAR MOTIONExercise:Revision Test
Explore 57 Videos
Similar Questions
Two slabs are of the thicknesses d1 and d2. Their thermal conductivities are K1 and K2 respectively They are in series. The free ends of the combination of these two slabs are kept at temperatures θ1 and θ2. Assume θ1>θ2. The temperature θ of their common junction is
View SolutionTwo vessels of different materials are similar in size and other respects. The same quantity of ice filled in them gets melted in 40 and 70 minutes respectively. The ration of thermal conductivities for the materials of boxes is :
View SolutionChoose the forward biased p-n junction :
View SolutionA sphere of mass m is tied to end of a string of length 1 and rotated through the other and along a horizontal circular path with speed . The work done in full horizontal circle is:
View SolutionA liquid in a beaker has temperature θ(t) at time t and θ0 is temperature of surroundings, then according to Newton's law of cooling the correct graph between loge(θ−θ0) and t is :
View SolutionA body with an initial temperature θ1 is allowed to cool in a surrounding which is at a constant temperature of θ0(θ<θ1) Assume that Newton's law of cooling is obeyed Let k= constant The temperature of the body after time t is best experssed by .
View SolutionA body at temperature θ0 having Newton's cooling constant K is placed in a surrounding having temperature T0 at time t = 0. The graph of temperature of the body as a function of time t is shown in the adjacent figure. A tangent on the curve is drawn at t = 0 as shown in the figure. Find the value of τ.

View Solutionएक बीकर में एक द्रव का ताप समय t पर θ है तथा वातावरण का ताप θ0 है तब न्यूटन के शीतलन नियम के अनुसार loge(θ−θ0) तथा t के बीच सही ग्राफ है:
View SolutionIf the temperature of the body theta and time of cooling 't' and room temperature of the surrounding theta_(0) . The cooling curve is
View SolutionIf a piece of metal is heated to temperature θ and then allowed to cool in a room which is at temperature θ0 the graph between the temperature T of the metal and time t will be closest to :
View Solutionएक बीकर में एक द्रव का तापमान समय t पर θ(t) है और वातावरण का तापमान θ0 है, तब न्यूटन के शीतलन नियम के अनुसार loge(θ−θ0) और t के बीच निम्न में से कौन सा ग्राफ सही है
View SolutionA liquid in a beaker has temperature θ(t) at time t and θ0 is temperature of surroundings, then according to Newton's law of cooling the correct graph between loge(θ−θ0) and t is :
View SolutionA body with an initial temperature θ, is allowed to cool in a surrounding which is at a constant temperature of θ0(θ0<θi). Assume that Newton.s law of cooling is obeyed. Let k = constant. The temperature of the body after time t is best expressed by
View SolutionA liquid in beaker has temperature θ(t) at time t and q0 is temperature of surroundings, then according to Newton's law of cooling, the correct graph between loge(θ−θ0) and t is
View SolutionA body with an initial temperature theta_(1) is allowed to cool in a surrounding which is at a constant temperature of theta_(0) (theta lt theta_(1)) Assume that Newton's law of cooling is obeyed Let k = constant The temperature of the body after time t is best experssed by .
View Solution

