Obtain the maximum kinetic energy of -particles, and the radiation frequencies of decays in the decay scheme shown in Fig. . You are given that
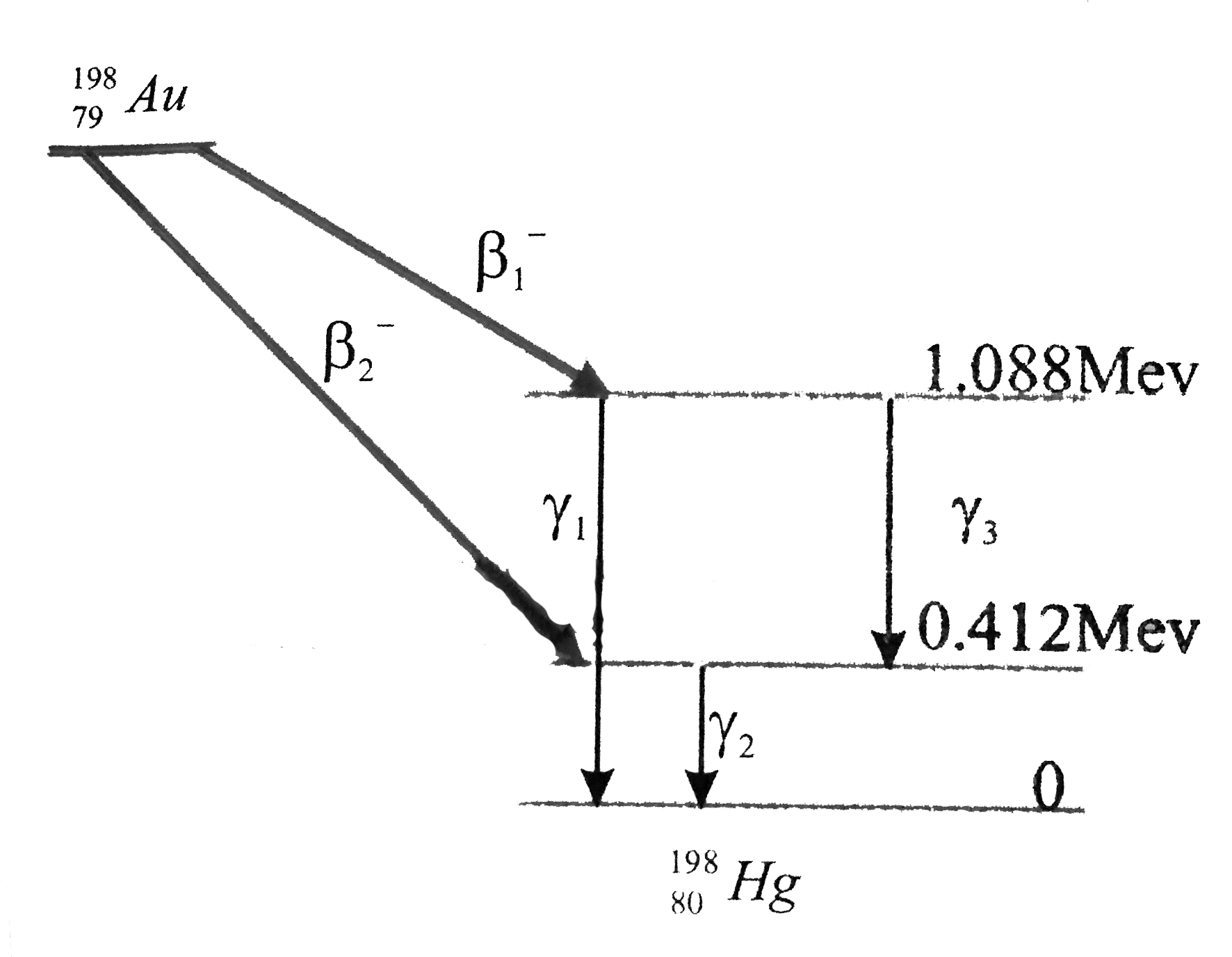
Beta decay equation for is
But
(Ignoring rest mass of antineutrino) where mN represents nuclear mass. In terms of atomic masses
Hence, K.E. of particles.
MeV
In transition, energy shared by
(from the given figure)
Max kinetic energy of (particle ignoring kinetic energy of )
MeV
In transition, K.E. shared by
MeV (from the given figure)
Mass kinetic energy of particle.
MeV
For transition, energy is given as follows:
J
Corresponding frequency is calculated as follows:
Hz
For transition, energy is given as follows:
MeV
J
Corresponding frequency is calculated as follows:
Hz
For
Hz.
Topper's Solved these Questions
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - NCERT FILE SOLVED (NCERT EXEMPLAR PROBLEMS SUBJECTIVE QUESTIONS) (VERY SHORT ANSWER TYPE QUESTIONS)
5 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - NCERT FILE SOLVED (NCERT EXEMPLAR PROBLEMS SUBJECTIVE QUESTIONS (SHORT ANSWER TYPE QUESTIONS))
5 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - NCERT FILE SOLVED (TEXTBOOK EXERCISES)
22 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - CHAPTER PRACTICE TEST
13 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
Calculate the kinetic energy of β-particles and the radiation frequencies corresponding to the γ-decays shown in figure.
Given, mass of .12Mg27 atom =26.991425 amu and mass of .13Al27 atom = 26.990080 amu

View SolutionCalculate the maximum kinetic energy of the bera particle emitted in the following decay scheme:
^12N rarr 12C∗+e++v
^12C rarr ^12C+γ(4.43MeV).
The atomic mass of 12Nis12.018612u.
View Solution
Knowledge Check
Gold .19879Au undergoes β− decay to an excited state of .19880Hg. If the excited state decays by emission of a γ-photon with energy 0.412MeV, the maximum kinetic energy of the electron emitted in the decay is (This maximum occurs when the antineutrino has negligible energy. The recoil energy of the .19880Hg nucleus can be ignored. The masses of the neutral atoms in their ground states are 197.968255u for .19879Hg).
A0.412MeVB1.371MeVC0.959MeVD1.473MeVGold nucleus (19879Au) can decay into mercuyr nucleus (19880Hg8) by two decay schemes shown in figure below (i) it can emit a β -particle (β1) and come to ground state by either emiting one γ- ray (γ1) or emitting two γ- rays (γ3 and γ4) (ii) It can emit one β- particle (β2) and come to ground state by emitting γ2 ray. Atomic masses: 198Au=197.9652 amu and 198Hg=197.9662 amu. Given that 1 amu= 930MeV/c2. The energy levels of the nucleus are shown in figure below
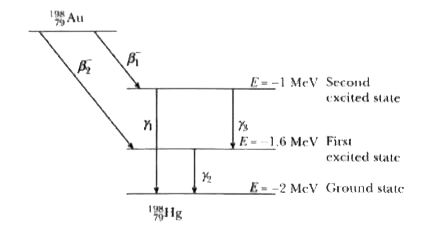
Whatis the maximum kinetic energy of emitted β2 particle?A1.44 MeVB0.59 MeVC1.86 MeVD1.46 MeVGold nucleus (19879Au) can decay into mercuyr nucleus (19880Hg8) by two decay schemes shown in figure below (i) it can emit a β -particle (β1) and come to ground state by either emiting one γ- ray (γ1) or emitting two γ- rays (γ3 and γ4) (ii) It can emit one β- particle (β2) and come to ground state by emitting γ2 ray. Atomic masses: 198Au=197.9652 amu and 198Hg=197.9662 amu. Given that 1 amu= 930MeV/c2. The energy levels of the nucleus are shown in figure below
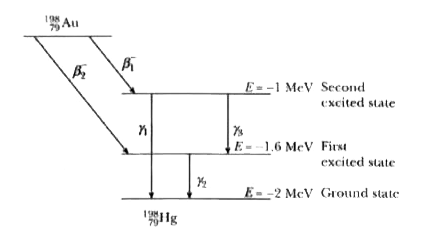
What is the maximum kinetic energy of emitted β1 parricle ?A1.28 MeVB0.77 MeVC1.86 MeVD0.86 MeV
Calculate the maximum energy that a β particle can have in the following decay:
.8O19→.9F19+.−1e0+¯¯¯V
Given, m(.8O19)=19.003576u,m(.9F19)=18.998403u,m(.−1e0)=0.000549u
View SolutionA nucleus 10Ne23 undergoes β- decay and becomes 11Na23 . Calculate the maximum kinetic energy of electrons emitted assuming that the daughter nucleus and antineutrino carry negligible kinetic energy. Given mass of 10Ne23 = 22.994466 u and mass of 11Na23 = 22.989770 m
View SolutionConsider one of the fission reactions of U235 by thernmal neutrons :
.92U235+n→.38Sr94+.54Ce140+2n
The fission fragments are, however, not stable. They unaergo successive β−decays unit .38Sr94 becomes .40Zr94 and .54Xe140 becomes .58Ce140. Estimate the total energy released in the process. Is all that energy available as kinetic energy of the fission products (Zr and Ce)? You are given that
m(U235)=255.0439amu, mn=1.00866amu m(Zr94)=93.9065amu, m(Ce140)=139.9055amu
View SolutionConsider the beta decay
^198Au→198Hg∗+Bη−1+→v.
where ^198Hg∗ represents a mercury nucleus in an excited state at energy 1.088MeV above the ground state. What can be the maximum kinetic energy of the electron emitted? The atomic mass of ^198Au is 197.968233u and that of ^198Hg is 197.966760u.
View SolutionGold nucleus (19879Au) can decay into mercuyr nucleus (19880Hg8) by two decay schemes shown in figure below (i) it can emit a β -particle (β1) and come to ground state by either emiting one γ- ray (γ1) or emitting two γ- rays (γ3 and γ4) (ii) It can emit one β- particle (β2) and come to ground state by emitting γ2 ray. Atomic masses: 198Au=197.9652 amu and 198Hg=197.9662 amu. Given that 1 amu= 930MeV/c2. The energy levels of the nucleus are shown in figure below
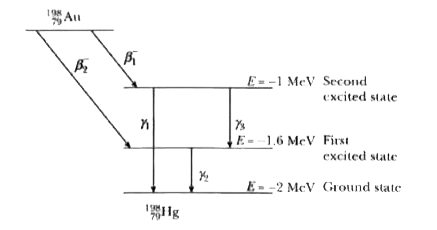
The wavelength of emitted γ - rays is the order
View Solution
