In the Bohr's model of hydrogen atom, the radius of nth orbit is proportional to na. Find the value of a if electric potential energy of the atom is given as :U=U0ln(rr0) . Here r0 and U0 are constant and r is the radius of the orbit in which electron is moving arounds the nucleus .
The correct Answer is:1
To find the value of a in the equation r∝na for the radius of the nth orbit in the Bohr model of the hydrogen atom, given the electric potential energy U=U0ln(rr0), we can follow these steps:
Step 1: Understand the relationship between potential energy and force
The electric potential energy U is related to the force acting on the electron. The force F can be expressed as:
F=−dUdr
Calculating the derivative of U with respect to r:
F=−ddr(U0ln(rr0))=−U0r
Step 2: Relate force to centripetal force
In the Bohr model, the centripetal force required to keep the electron in circular motion is provided by the electrostatic force between the electron and the nucleus:
F=mv2r=ke2r2
where k is Coulomb's constant, e is the charge of the electron, and m is the mass of the electron.
Step 3: Set the forces equal
Equating the two expressions for force:
−U0r=mv2r
This implies:
U0=−mv2
Step 4: Use Bohr's quantization condition
According to Bohr's model, the angular momentum L of the electron is quantized:
L=mvr=nh2π
From this, we can express the velocity v:
v=nh2πmr
Step 5: Substitute v into the energy equation
Substituting this expression for v into the equation U0=−mv2:
U0=−m(nh2πmr)2
This simplifies to:
U0=−n2h24π2r
Step 6: Rearranging for r
Rearranging the equation gives:
r=−n2h24π2U0
This shows that r is proportional to n2:
r∝n2
Step 7: Identify the value of a
From the relationship r∝na, we have found that r∝n2. Thus, we can conclude:
a=2
Final Answer
The value of a is 2.
---
The electric potential energy U is related to the force acting on the electron. The force F can be expressed as:
F=−dUdr
Calculating the derivative of U with respect to r:
F=−ddr(U0ln(rr0))=−U0r
In the Bohr model, the centripetal force required to keep the electron in circular motion is provided by the electrostatic force between the electron and the nucleus:
F=mv2r=ke2r2
where k is Coulomb's constant, e is the charge of the electron, and m is the mass of the electron.
Equating the two expressions for force:
−U0r=mv2r
This implies:
U0=−mv2
According to Bohr's model, the angular momentum L of the electron is quantized:
L=mvr=nh2π
From this, we can express the velocity v:
v=nh2πmr
Substituting this expression for v into the equation U0=−mv2:
U0=−m(nh2πmr)2
This simplifies to:
U0=−n2h24π2r
Rearranging the equation gives:
r=−n2h24π2U0
This shows that r is proportional to n2:
r∝n2
From the relationship r∝na, we have found that r∝n2. Thus, we can conclude:
a=2
The value of a is 2.
Topper's Solved these Questions
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - COMPETITION FILE (Ncert Exemplar Problems )
13 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - COMPETITION FILE (Matrix match )
2 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Chapter Practice Test
15 Videos
Similar Questions
Derive an expression for the radius of nth Bohr’s orbit in Hydrogen atom.
View SolutionIn a hypothetical hydrogen atom the electrostatic potential energy of interaction of proton and electron is given by U=U0ln(rr0) where U0 and r0 are constants and r is radius of circular orbit of electron. For such hydrogen atom the energy difference between nth and mth state is represented by ΔEnm. Calculate the ratio ΔE12:ΔE24 Assume Bohr’s assumption of angular momentum quantization to hold.
View Solution
Knowledge Check
In the Bohr's hydrogen atom model, the radius of the stationary orbit is directly proportional to (n = principal quantum number)
An−1BnCn−2Dn2In hydrogen atom, the radius of nth Bohr orbit is Vn. The graph Beetween log.(rnr1) will be
A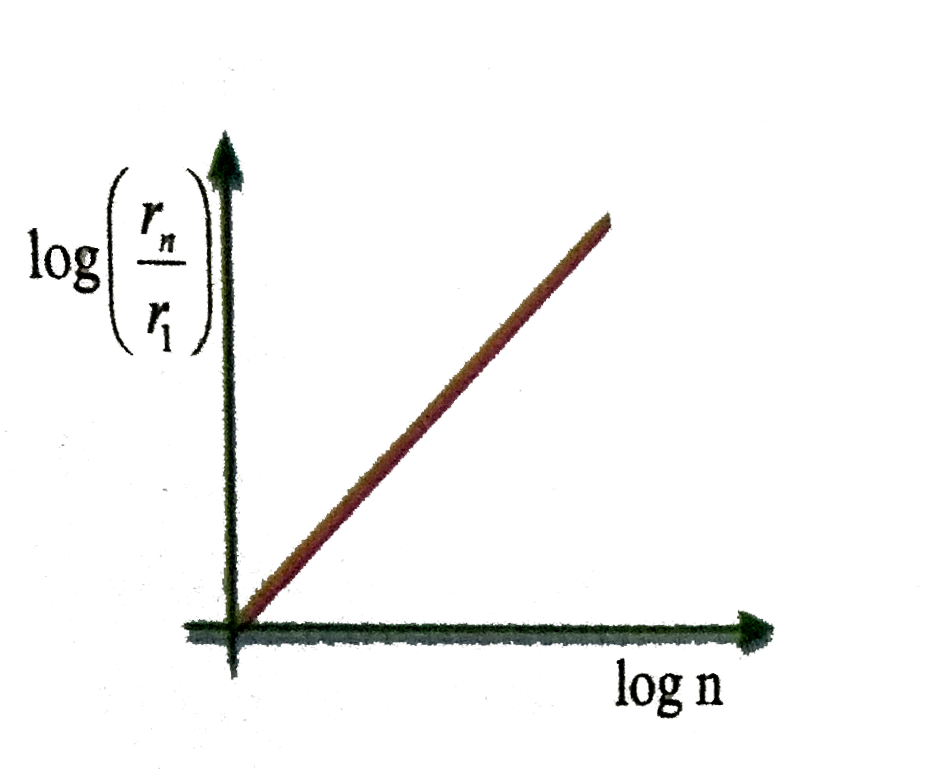 B
B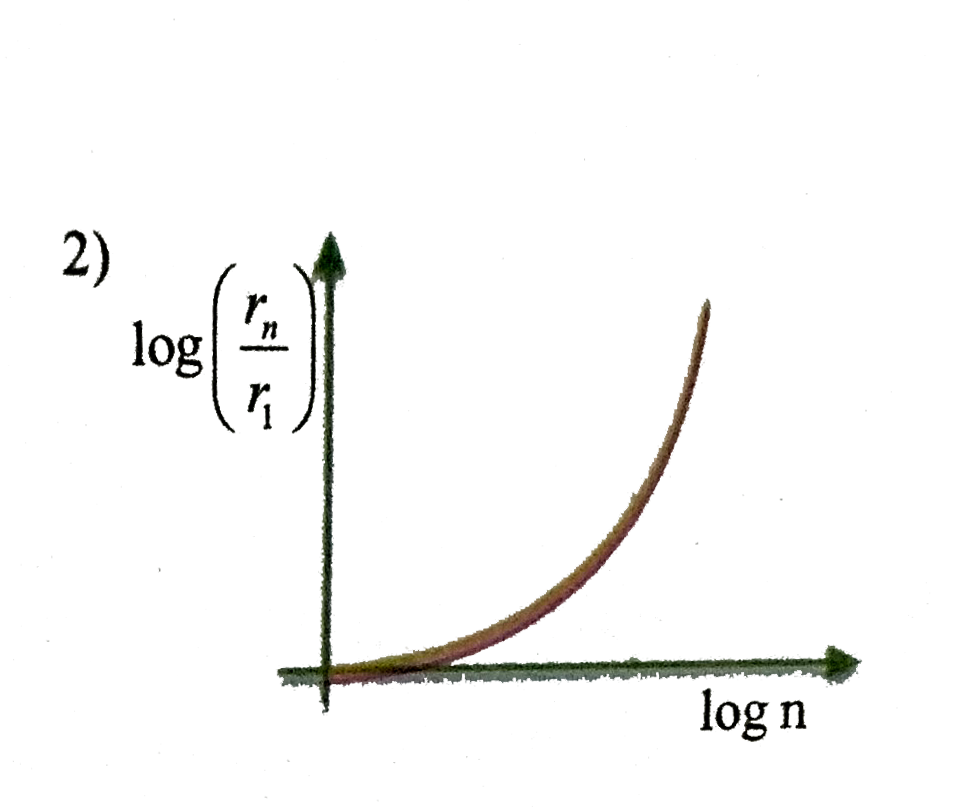 C
C D
D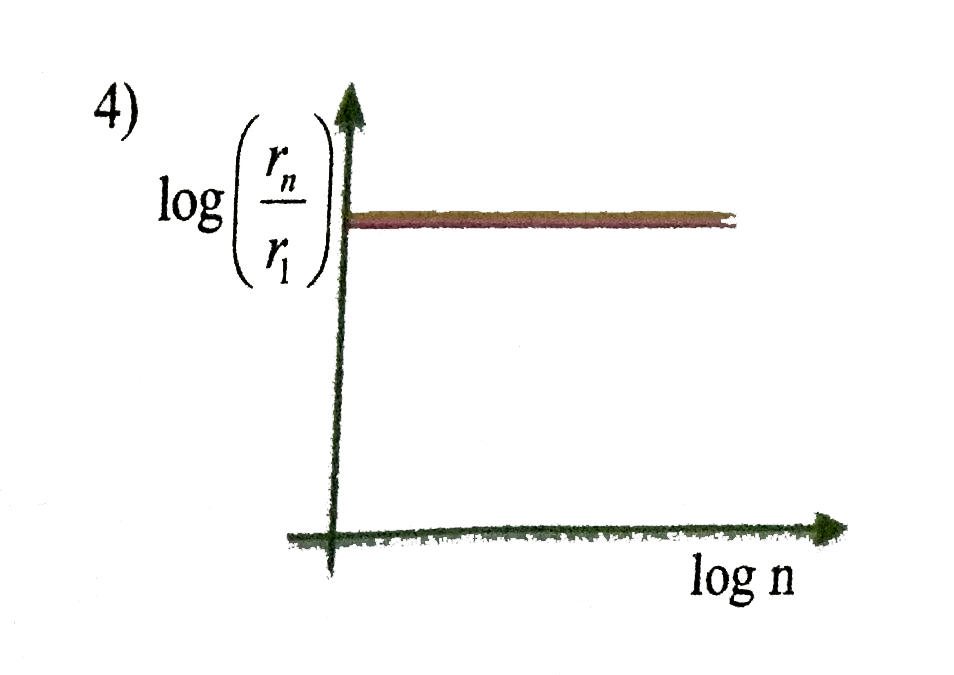
In Bohr's model, if the atomic radius of the first orbit is r0, then the radius of the fourth orbit is
Ar0B4r0Cr0/16D16r0
In Bohr's mode, the atomic radius of the first orbit is r0 then the radius of the third orbit is
View SolutionIf in hydrogen atom, radius of nth Bohr orbit is rn., frequency of revolution of electron in nth orbit is fn choose the correct option.
View SolutionIf the radius of the second Bohr of hydrogen atom is r2 the radius of the third Bohr orbit will be
View SolutionIf the radius of first Bohr orbit is r, the wavelength of an electron in the third orbit of a hydrogen atom is equal to
View SolutionIf 'r' is the radius of the lowest orbit of Bohr's model of H-atom, then the radius of nth orbit is
View Solution
