Show that average value of radiant flux density S over a single period 'T' is given by S=12cμ0E20.
Radiant flux density .S. , also known as poynting vector , is given by
→S=1μ0(→E×→B)
where →E and →B are electric field vector and magnetic field , respectively .
Also 1μ0=c2ε0 [∴c=1√μ0eπs0]
∴→S=−c2ε0(→E×→B)
Let us consider that the electromagnetic wave is propargating along the X - axis and the electric field vector →E is along the Y - axis and the electric field vector →B is along the Z- axis
∴→E=(E0cos(kx−ωt)ˆj
→B=(B0cos(kx−ωt)ˆk
⇒→E×→B=(E0B0)cos2(kx−ωt)(ˆj׈k)
∴→S=c2ε0(E0B0)cos2(kx−ωt)(ˆi)
Over the complete cycle ( time interval T) . the average value of the magnitude of radiant flux density is given by
Sav=c2ε0(E0B0)1T∫T0cos2(kx−ωt)dt
since ∫T0cos2(kx−ωt)dt−T2
∴SAv=c2ε0E0×B0×1T×T2
⇒SAv=c2ε0E0B02
=c2ε0E02×E0c[∴B0=E0C]=cε0E202
=12×cc2μ0E20[ε0=1c2μ0]
⇒Sav=E202μ0C
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - HIGHER ORDER THINKING SKILS & ADVANCED LEVEL5videos
ELECTROMAGNETIC WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - REVISION EXERCISES ( VERY SHORT ANSWER QUESTIONS)46videos
ELECTROMAGNETIC WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - NCERT FILE ( NCERT EXEMPLAR PROBLEMS SUBJECTIVE QUESTIONS ) ( VERY SHORT ANSWER TYPE QUESTIONS )7videos
ELECTROMAGNETIC WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION14videos
ELECTROMAGNETIC INDUCTION
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Chapter Practice Test9videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
Similar Questions
A plane EM wave travelling along z direction is described by
E=E0sin(kz−ωt)ˆiandB=B0sin(kz−ωt)ˆj.
show that
(i) The average energy density of the wave is given by uav=14ε0E20+14B20μ0.
(ii) The time averaged intensity of the wave is given by Iav=12cε0E20.View SolutionShow that average energy density of electromagnetic radiation can be written as ε0E2rms .
View Solution
Knowledge Check
- Question 1 - Select One
The average value of current for the current shown for time period 0 to T2 s
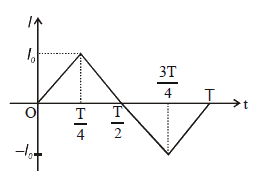 Al0√2Bl02Cl0√3Dl02√3
Al0√2Bl02Cl0√3Dl02√3 - Question 2 - Select One
Poynting vectors →S is defined as →S=1μ0→E×→B. The average value of '→S' over a single period 'T' is given by
AE20/2cμ0BE20/cμ0C2E022/cμ0DE20/cμ20 - Question 3 - Select One
Assertion (A) : The average value of <sin2ωt> is zero.
Reason (R ) : The average value of function F(t) over a period T is <F(t)>=1T∫T0F(t)dtABoth Assertion and Reason are true and Reason is the correct explanation of Assertion.BBoth Assertion and Reason are true but Reason is not the correct explanation of Assertion.CAssertion is true but Reason is falseDAssertion is false but Reason is true
A closed coil having 50 turns, area 300cm2, is rotated from a position where it plane makes an angle of 45∘ with a magnetic field of flux density 2.0T to a position perpendlcular to the field in a time of 0.1s. What is the average EMF induced in the coil ?
View SolutionDetermine the average value of the electromotive force Em over one period, ie, over the time from t= 0 to t=T, if electromotive force is computed by the formula
E=E0 sin 2πtT
where T is the duration of the period in seconds, E0 the amplitude (the maximum value) of the electromotive force corresponding to the value t= 0.25T. The fraction 2πtT is called the phase.View SolutionThe average value of a saw-tooth voltage V=V0(2tT−1) Over 0 to T2, (T- time period) is given by
View SolutionA particle performing S.H.M. with amplitude 'A' and period T. The average values of magnitude of distance over a half period is
View SolutionThe average value of a.c. voltge E=E0sinωt over the time interval t = 0 to t = π/ω is
View Solution
