What should be the rate of change of potential difference across a parallel plate capacitor of 2μF , so that displacement current of 1A flows through it ?
To find the rate of change of potential difference across a parallel plate capacitor such that a displacement current of 1 A flows through it, we can follow these steps:
1. Understand the relationship between displacement current and electric field:
The displacement current ID can be expressed in terms of the rate of change of electric field dEdt and the area A of the plates:
ID=ϵ0AdEdt
where ϵ0 is the permittivity of free space.
2. Relate electric field to potential difference:
The electric field E between the plates of a capacitor is related to the potential difference V and the distance d between the plates:
E=Vd
Therefore, the rate of change of electric field can be expressed as:
dEdt=1ddVdt
3. Substitute dEdt into the displacement current equation:
Substituting dEdt into the equation for displacement current gives:
ID=ϵ0A(1ddVdt)
4. Rearranging the equation:
Rearranging the equation to find dVdt:
dVdt=ID⋅dϵ0A
5. Substituting known values:
Given:
- Displacement current ID=1A
- Capacitance C=2μF=2×10−6F
- The relationship C=ϵ0Ad allows us to express ϵ0A in terms of C and d:
ϵ0A=C⋅d
6. Final substitution:
Substituting ϵ0A into the equation for dVdt:
dVdt=ID⋅dC
Since we don't have the distance d, we can express dVdt in terms of C:
dVdt=1A2×10−6F=5×105V/s
Conclusion:
The required rate of change of potential difference across the capacitor is:
dVdt=5×105V/s
The displacement current ID can be expressed in terms of the rate of change of electric field dEdt and the area A of the plates:
ID=ϵ0AdEdt
where ϵ0 is the permittivity of free space.
The electric field E between the plates of a capacitor is related to the potential difference V and the distance d between the plates:
E=Vd
Therefore, the rate of change of electric field can be expressed as:
dEdt=1ddVdt
Substituting dEdt into the equation for displacement current gives:
ID=ϵ0A(1ddVdt)
Rearranging the equation to find dVdt:
dVdt=ID⋅dϵ0A
Given:
- Displacement current ID=1A
- Capacitance C=2μF=2×10−6F
- The relationship C=ϵ0Ad allows us to express ϵ0A in terms of C and d:
ϵ0A=C⋅d
Substituting ϵ0A into the equation for dVdt:
dVdt=ID⋅dC
Since we don't have the distance d, we can express dVdt in terms of C:
dVdt=1A2×10−6F=5×105V/s
The required rate of change of potential difference across the capacitor is:
dVdt=5×105V/s
Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CONCEPTUAL QUESTIONS
12 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - TOUGH & TRICKY PROBLEMS
4 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Chapter Practice Test
9 Videos
Similar Questions
Knowledge Check
In the circuit shown in the figure, the potential difference across the 4.5μF capacitor is
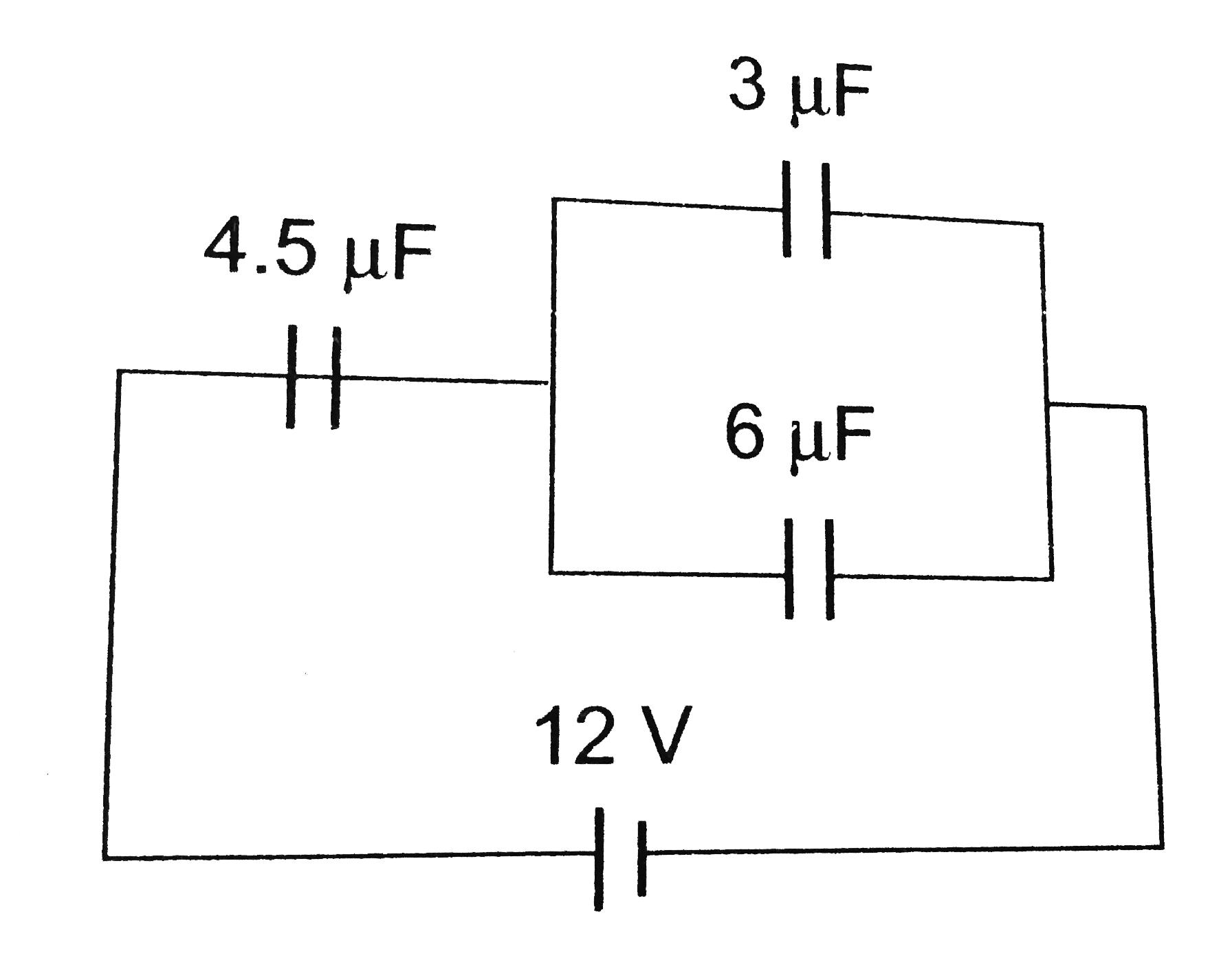 A8/3 voltB4 voltC6voltD8volt
A8/3 voltB4 voltC6voltD8voltAt what rate the potential difference between the plates of a parallel plate capacitance 2μF should be changed to establish a displacement current of 2mA between its plates?
A2×102V/sB2×103V/sC103V/sD2×10−3V/sThe rate of change of voltage of a parallel plate capacitor if the instantaneous displacement current of 1A is established between the two plates of a 1µF parallel plate capacitor
A106 v/sB10 v/sC108 v/sD10–6 v/s
In the circuit shown in the following the potential difference across the 3μF capacitor is
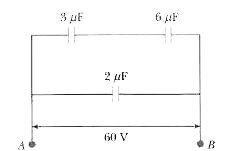
View SolutionYou are given a 2μF parallel plate capacitor. How would you establish an instantaneous displacement current fo 1mA in the space between its plates?
View SolutionThe voltage between the plates of a parallel plate capacitor of capacitance 1.0μFis changing at rate of 1.0V/s. Find displacement current
View SolutionA capacitor consists of two circular plates each of radius 8.0 cm and separated by 3.0 mm. The capacitor is being charged by an external battery. The charging current is constant and is equal to 0.3 A. Calculate (i) capacitance of capacitor, (ii) the rate of change of potential difference across the plates of capacitor and (iii) the displacement current.
View SolutionThe potential difference between the plates of a parallel plate capacitor of capacitance 2μF is changing at the rate of 105V/s. What is the displacement current in the dielectric of the capacitor?
View Solution

