Current flowing through an inductor as a function of time is given as follows :
I = 4 + 16 t. here I is in amperes and t is in seconds. Emf induced in the inductor is 20 mV.
Rate of energy supplied to inductor at t = 2 s is
0.36 W
0.72 W
1.44 W
2.88 W
The correct Answer is:B
To solve the problem step by step, we will follow these steps:
Step 1: Understand the given current function
The current flowing through the inductor is given by the equation:
I(t)=4+16t
where I is in amperes and t is in seconds.
Step 2: Calculate the current at t=2 seconds
To find the current at t=2 seconds, substitute t=2 into the current function:
I(2)=4+16(2)
I(2)=4+32
I(2)=36A
Step 3: Understand the induced EMF
The induced EMF in the inductor is given as:
EMF=20mV=20×10−3V
Step 4: Calculate the power supplied to the inductor
The rate of energy supplied (power) to the inductor can be calculated using the formula:
P=EMF×I
Substituting the values we have:
P=(20×10−3V)×(36A)
P=0.72W
Final Answer
The rate of energy supplied to the inductor at t=2 seconds is:
P=0.72W
---
The current flowing through the inductor is given by the equation:
I(t)=4+16t
where I is in amperes and t is in seconds.
To find the current at t=2 seconds, substitute t=2 into the current function:
I(2)=4+16(2)
I(2)=4+32
I(2)=36A
The induced EMF in the inductor is given as:
EMF=20mV=20×10−3V
The rate of energy supplied (power) to the inductor can be calculated using the formula:
P=EMF×I
Substituting the values we have:
P=(20×10−3V)×(36A)
P=0.72W
The rate of energy supplied to the inductor at t=2 seconds is:
P=0.72W
Topper's Solved these Questions
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:COMPETITION FILE ASSERTION REASON TYPE QUESTIONS
Explore 10 Videos
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:COMPETITION FILE INTEGER TYPE QUESTIONS
Explore 11 Videos
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:COMPETITION FILE C. MULTIPLE CHOICE QUESTIONS
Explore 17 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
Similar Questions
Find the time in which the current changes from 3 A to 1 A through an inductor of 10 H. The emf induced in the inductor is 20 V. Also, find the magnetic flux linked with the inductor.
View SolutionThe potential difference across a 2H inductor as a function of time is shown in figure. At time t=0, current is zero
Current t=2 second is
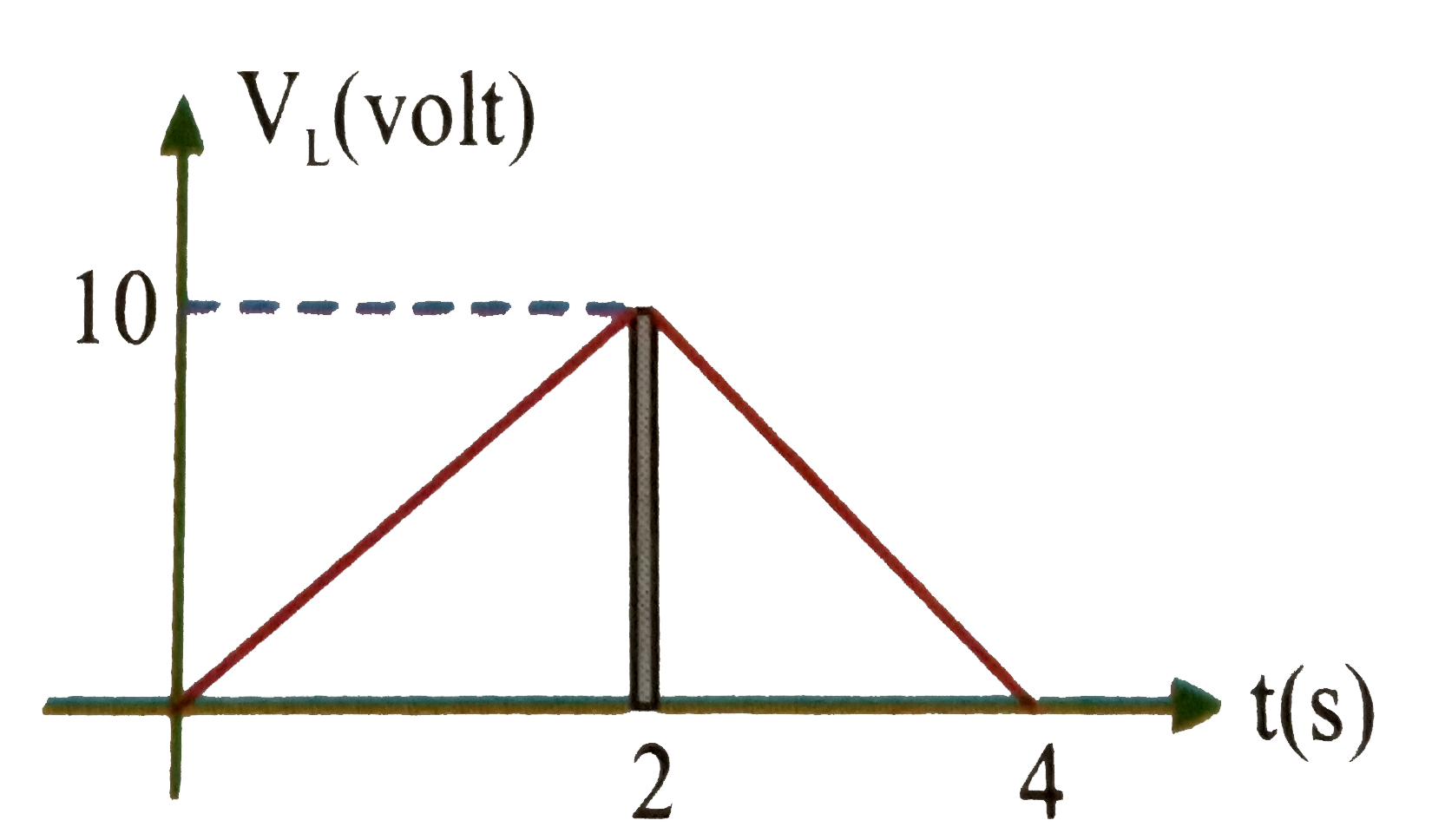
View Solution
Knowledge Check
Current flowing through an inductor as a function of time is given as follows :
I = 4 + 16 t. here I is in amperes and t is in seconds. Emf induced in the inductor is 20 mV.
What is self-inductance of the inductor ?A1.25 ×10−3 HB2.5×10−4 HC1.25×10−4 HD5×10−3 HThe current in a 90mH inductor changes with time as i=1.0t2, where I is in amperes and t is in seconds.
Athe magnitude of the induced emf at t=4.0s is 180 mVBthe emf zero at time t=3.0sCthe magnitude of the induced emf at t=4.0s is 360 mVDthe emf zero at time t=4.0sThe current in ampere through an inductor is
i(10+20t)
Here t is in second. The induced emf in the inductor 4V.
Total flux linked with the inductor at t= 2 isA10 WbB20 WbC30 WbD40 Wb
Current flowing through a conducting wire is given by
I=(1+2t)
Where t is in seconds and current I is in amperes. The charge (in coulombs) flown through the resistor in the interval from t=0 to t=1 second is -
View SolutionIn an inductor, the current / varies with time to l=5A+16.(A/s)t. If-induced emf in the induct is 5 mV, the self inductance of the inductor is
View SolutionIf the current through an inductor of 2 H is given by I=tsintA, then the voltage across the inductor is
View SolutionThe potential difference across a 10H inductor as a function of time is shown in the figure. At t=0 current is zero. Then
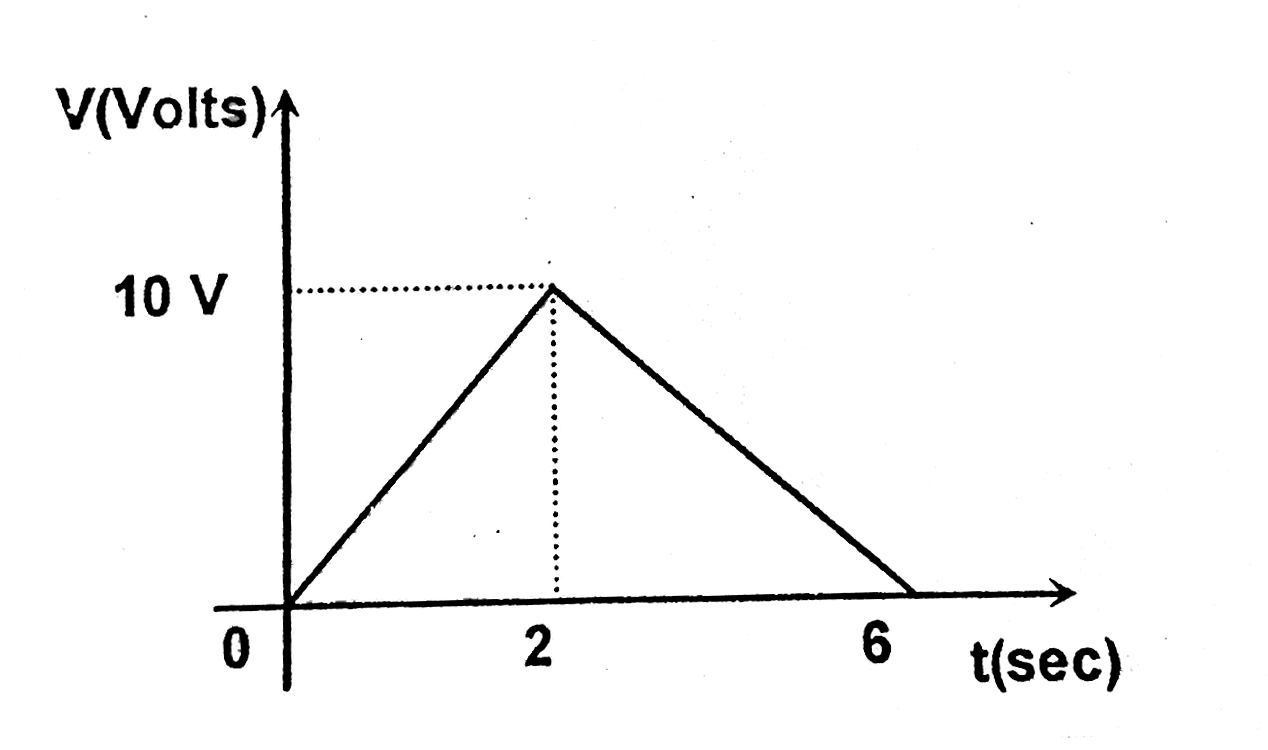
View SolutionThe potential difference a 2H inductor as a function of time is shown in figure. At time t=0, current is zero
Current versus time graph across the inductor will be
View Solution
