An LC circuit oscillating at natural frequency conssts of an inductor of inductance 30 m H and a capacitor of capacitance 60μF. The maximum value of instantaneous charge on capacitor in the circuit is 200 μC . If I is the current in the circuit then answer the following :
(i) What is the value of dIdt when charge is 150 μC?
(ii) Calculate the value of I when charge is 200 μC .
(iii) Find the maximum value of I.
(iv) For what value of q I is half of its maximum value ?
To solve the problem step-by-step, let's break it down into the parts as requested.
Given Data:
- Inductance L=30mH=30×10−3H
- Capacitance C=60μF=60×10−6F
- Maximum charge on the capacitor Q0=200μC=200×10−6C
Natural Frequency Calculation:
The natural frequency ω of an LC circuit is given by:
ω=1√LC
Substituting the values:
ω=1√(30×10−3)(60×10−6)=1√1.8×10−6=11.3416×10−3≈744.6rad/s
(i) Calculate dIdt when charge q=150μC:
1. The charge q in an LC circuit can be expressed as:
q(t)=Q0sin(ωt)
Therefore, the current I is given by:
I=dqdt=Q0ωcos(ωt)
2. To find dIdt:
dIdt=ddt(Q0ωcos(ωt))=−Q0ω2sin(ωt)
3. We need to find sin(ωt) when q=150μC:
150×10−6=200×10−6sin(ωt)⟹sin(ωt)=150200=0.75
4. Now, using sin2(ωt)+cos2(ωt)=1:
cos(ωt)=√1−sin2(ωt)=√1−(0.75)2=√0.4375≈0.6614
5. Substitute into dIdt:
dIdt=−200×10−6×(744.6)2×0.75
dIdt≈−200×10−6×554,000×0.75≈−82.4A/s
(ii) Calculate the value of I when charge is 200μC:
1. When q=200μC, sin(ωt)=1:
I=Q0ωcos(ωt)=200×10−6×744.6×0=0A
(iii) Find the maximum value of I:
1. The maximum current Imax occurs when cos(ωt)=1:
Imax=Q0ω=200×10−6×744.6≈0.149Aor149mA
(iv) For what value of q is I half of its maximum value?
1. Half of the maximum current:
I=Imax2=149mA2≈74.5mA
2. Setting the equation:
74.5×10−3=Q0ωcos(ωt)
74.5×10−3=200×10−6×744.6cos(ωt)
cos(ωt)=74.5×10−3149×10−3=0.5
3. Therefore, ωt=60∘ or π3.
4. Now, substitute back to find q:
q=Q0sin(ωt)=200×10−6sin(60∘)=200×10−6×√32≈173.2μC
Summary of Answers:
1. dIdt when q=150μC≈−82.4A/s
2. I when q=200μC=0A
3. Maximum I≈149mA
4. q when I is half of its maximum value ≈173.2μC
- Inductance L=30mH=30×10−3H
- Capacitance C=60μF=60×10−6F
- Maximum charge on the capacitor Q0=200μC=200×10−6C
The natural frequency ω of an LC circuit is given by:
ω=1√LC
Substituting the values:
ω=1√(30×10−3)(60×10−6)=1√1.8×10−6=11.3416×10−3≈744.6rad/s
1. The charge q in an LC circuit can be expressed as:
q(t)=Q0sin(ωt)
Therefore, the current I is given by:
I=dqdt=Q0ωcos(ωt)
2. To find dIdt:
dIdt=ddt(Q0ωcos(ωt))=−Q0ω2sin(ωt)
3. We need to find sin(ωt) when q=150μC:
150×10−6=200×10−6sin(ωt)⟹sin(ωt)=150200=0.75
4. Now, using sin2(ωt)+cos2(ωt)=1:
cos(ωt)=√1−sin2(ωt)=√1−(0.75)2=√0.4375≈0.6614
5. Substitute into dIdt:
dIdt=−200×10−6×(744.6)2×0.75
dIdt≈−200×10−6×554,000×0.75≈−82.4A/s
1. When q=200μC, sin(ωt)=1:
I=Q0ωcos(ωt)=200×10−6×744.6×0=0A
1. The maximum current Imax occurs when cos(ωt)=1:
Imax=Q0ω=200×10−6×744.6≈0.149Aor149mA
1. Half of the maximum current:
I=Imax2=149mA2≈74.5mA
2. Setting the equation:
74.5×10−3=Q0ωcos(ωt)
74.5×10−3=200×10−6×744.6cos(ωt)
cos(ωt)=74.5×10−3149×10−3=0.5
3. Therefore, ωt=60∘ or π3.
4. Now, substitute back to find q:
q=Q0sin(ωt)=200×10−6sin(60∘)=200×10−6×√32≈173.2μC
1. dIdt when q=150μC≈−82.4A/s
2. I when q=200μC=0A
3. Maximum I≈149mA
4. q when I is half of its maximum value ≈173.2μC
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - PRACTICE PROBLEMS
67 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - CONCEPTUAL QUESTIONS
25 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
Similar Questions
Knowledge Check
An a.c. circuit consists of an inductor of inductance 0.5 H and a capacitor of capacitance 8 uF in series. The current in the circuit is maximum when the angular frequency of a.c. source is
A500rads−1B4000rads−1C5000rads−1D2×106rads−1An AC circuit consists of an inductor of inductance 0.5H and a capacitor of capacitance 8μF in series. The current in the circuit is maximum when the angular frequency of AC source is
A500rad/secB2×105rad/secC4000rad/secD5000rad/secAn oscillator circuit contains an inductor 0.05 H and a capacitor of capacity 80μF. When the maximum voltage across the capacitor is 200 V, the maximum current (in amperes) in the circuit is
A4B8C10D16
An inductor of inductance 2 mH is connected across a charged capacitor of 5 μ F . Let q denote the instaneous charge on the capacitor and i the current in the circuit . Maximum value of q is Q = 200 μ C.
(a) When q = 100 μ C what is the value of /di/dt / ?
(b) When q = 200 μ C what is the value of i ?
View SolutionAn inductance of 1mH and a charged capacitor capacitance of 10 mu F are connected across each other.The resonating angular frequency of circuit is
View SolutionA 8μHinductor is shorted across a 2μF capacitor. The capacitor is initially charged to 20 V. The maximum value of the current in the circuit is
View SolutionThe charge on the 6 μF . Capacitor in the circuit shown is
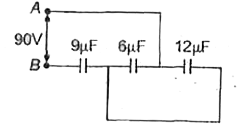
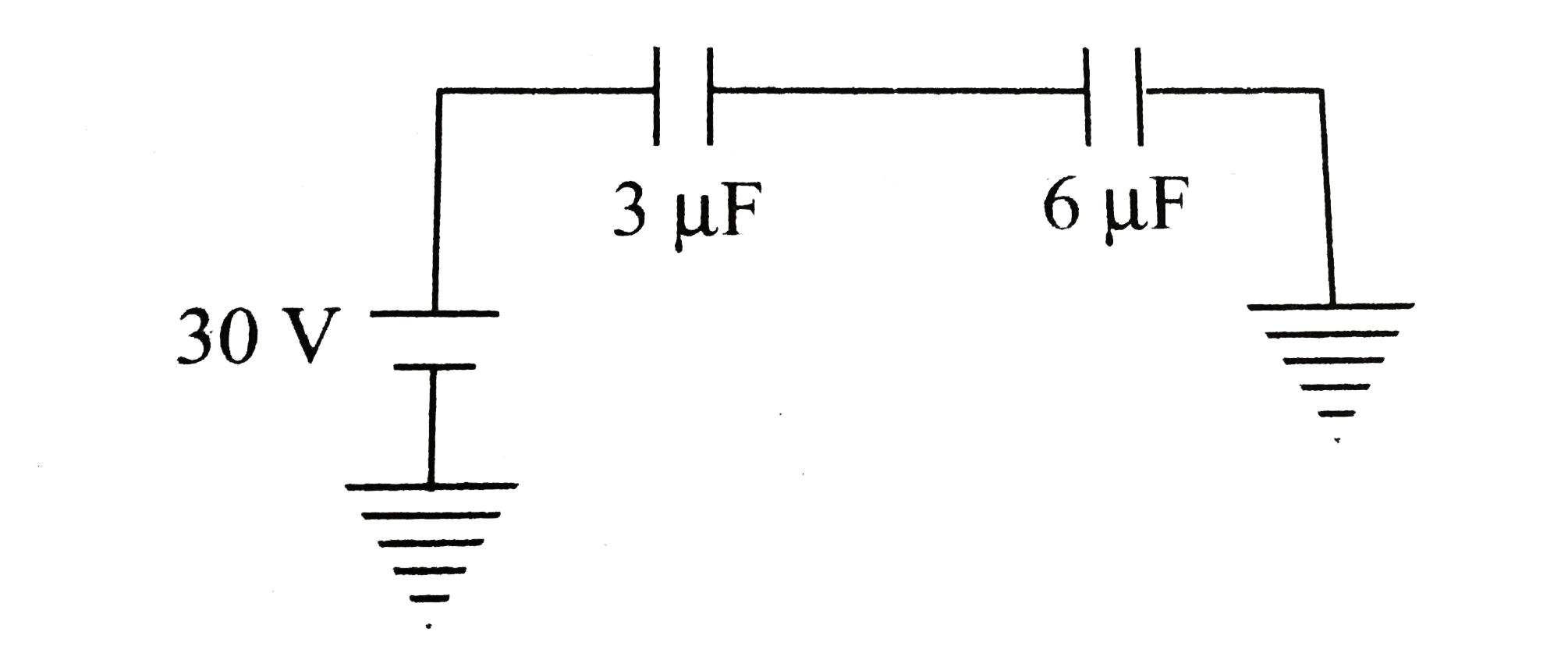
View SolutionIn the circuit shown in figure, the charge stored on a capacitor of capacitance 3μF is
View Solution