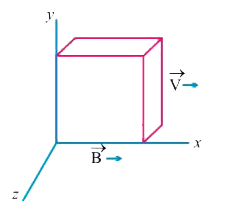
A cube consisting of 12 wires is moving with a velocity v in the direction of magnetic field. What will be the induced emf in each arm of the cube?
To solve the problem of finding the induced EMF in each arm of a cube consisting of 12 wires moving with a velocity v in the direction of a magnetic field B, we can follow these steps:
1. Understanding the Situation:
- We have a cube made up of 12 wires.
- The cube is moving with a velocity v in the same direction as the magnetic field B.
2. Identifying the Angle:
- Since the cube is moving in the direction of the magnetic field, the angle θ between the velocity vector v and the magnetic field vector B is 0∘.
3. Using the Formula for Induced EMF:
- The induced EMF (E) in a wire moving in a magnetic field can be calculated using the formula:
E=B⋅l⋅v⋅sin(θ)
- Here, B is the magnetic field strength, l is the length of the wire, v is the velocity, and θ is the angle between v and B.
4. Substituting the Values:
- Since θ=0∘, we have:
sin(0∘)=0
- Therefore, the induced EMF becomes:
E=B⋅l⋅v⋅0=0
5. Conclusion:
- Since the induced EMF is 0, there is no induced EMF in each arm of the cube.
Final Answer:
The induced EMF in each arm of the cube is 0.
---
- We have a cube made up of 12 wires.
- The cube is moving with a velocity v in the same direction as the magnetic field B.
- Since the cube is moving in the direction of the magnetic field, the angle θ between the velocity vector v and the magnetic field vector B is 0∘.
- The induced EMF (E) in a wire moving in a magnetic field can be calculated using the formula:
E=B⋅l⋅v⋅sin(θ)
- Here, B is the magnetic field strength, l is the length of the wire, v is the velocity, and θ is the angle between v and B.
- Since θ=0∘, we have:
sin(0∘)=0
- Therefore, the induced EMF becomes:
E=B⋅l⋅v⋅0=0
- Since the induced EMF is 0, there is no induced EMF in each arm of the cube.
The induced EMF in each arm of the cube is 0.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:REVISION EXERCISE (Long Answer Questions)
Explore 9 Videos
- ELECTROMAGNETIC INDUCTIONBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:REVISION EXERCISE (Numerical Problems)
Explore 16 Videos
- ELECTROMAGNETIC INDUCTIONBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:REVISION EXERCISE (Fill in the blanks)
Explore 7 Videos
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Chapter Practice Test
Explore 15 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
Twelve wires of equal lengths are connected in the form of a skeleton of a cube, which is moving with a velocity →V in the direction of magnetic field →B. Find the emf in each arm of the cube.
View SolutionA glass rod of length l moves with velocity in a uniform magnetic field B. What is the e.m.f. induced in the rod ?
View Solution
Knowledge Check
A wire is moving with velocity 12×10−2m/s in a magnetic field of 0.5 T. if the induced emf is 9 mV, the length of wire is
A150 cmB15 cmC1.5 cmD0.15 cmA conductor PQ , with PQ=r , moves with a velocity v in a uniform magnetic field of induced B . The emf induced in the rod is
A(→v×→B).→rB→v.(→r×→B)C→B.(→r×→v)D∣∣→r×(→v×→B)∣∣A conduting wire ABC (as shown) is moving with a constant velocity along horizontal direction. The magnetic field is perpendicular to the wire and directed into the page. AB =BC. Find the range of angle (θ) made by rod AB with horizontal at A so that value of induced emf at A is greater than at C
 Aθ>45∘Bθ<45∘Cθ>60∘Dθ<75∘
Aθ>45∘Bθ<45∘Cθ>60∘Dθ<75∘
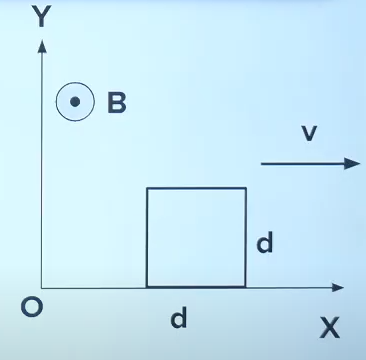
A square loop of side d is moved with velocity vˆi in an non-uniform magnetic field B0axˆk then the emf induced shown is?
View SolutionA wire moves with some speed perpendicular to a magnetic field. Why is emf induced across the rod?
View SolutionA two metre wire is moving with a velocity of 1 m/sec perpendicular to a magnetic field of 0.5weber/m2. The e.m.f. induced in it will be
View SolutionA conductor is moving with the velocity v in the magnetic field and induced current is I. If the velocity of conductor becomes double, the induced current will be
View SolutionA semicircle loop PQ of radius 'R' is moved with velocity 'v' in transverse magnetic field as shown in figure . The value of induced emf . Between the ends of loop is :-
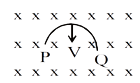
View Solution

