There is one square loop of area 0.5 m2 coplanar with a long straight wire in which a current of 20 ampere is flowering. Distance of the loop from the wire is 30. If current in the wire changes from 20 A to 0 in time 0.5 a. What will be the average emf induced in the loop ?
The correct Answer is:1.33×10−11V
To solve the problem of finding the average emf induced in a square loop due to a changing current in a nearby straight wire, we can follow these steps:
1. Identify Given Values:
- Area of the square loop, A=0.5m2
- Initial current in the wire, I1=20A
- Final current in the wire, I2=0A
- Distance from the wire to the loop, d=30cm=0.3m
- Time duration for the change in current, Δt=0.5s
2. Calculate the Change in Current:
ΔI=I2−I1=0−20=−20A
3. Determine the Rate of Change of Current:
dIdt=ΔIΔt=−20A0.5s=−40A/s
4. Calculate the Magnetic Field (B) due to the Wire:
The magnetic field at a distance d from a long straight wire carrying current I is given by:
B=μ04π⋅2Id
where μ0=4π×10−7T⋅m/A.
Substituting the values:
B=(4π×10−7)4π⋅2×200.3=10−7⋅400.3=4×10−60.3=4×10−60.3≈1.33×10−5T
5. Calculate the Induced EMF:
According to Faraday's law of electromagnetic induction, the induced emf (E) in the loop is given by:
E=−A⋅dBdt
Since B is changing due to the changing current, we can express dBdt in terms of dIdt:
dBdt=μ04π⋅2d⋅dIdt
Substituting the values:
dBdt=(4π×10−7)4π⋅20.3⋅(−40)=10−7⋅2⋅(−40)0.3
=−8×10−70.3=−2.67×10−6T/s
Now substituting into the emf equation:
E=−0.5⋅(−2.67×10−6)=1.33×10−6V
Final Answer:
The average emf induced in the loop is approximately:
E≈1.33×10−6V
- Area of the square loop, A=0.5m2
- Initial current in the wire, I1=20A
- Final current in the wire, I2=0A
- Distance from the wire to the loop, d=30cm=0.3m
- Time duration for the change in current, Δt=0.5s
ΔI=I2−I1=0−20=−20A
dIdt=ΔIΔt=−20A0.5s=−40A/s
The magnetic field at a distance d from a long straight wire carrying current I is given by:
B=μ04π⋅2Id
where μ0=4π×10−7T⋅m/A.
B=(4π×10−7)4π⋅2×200.3=10−7⋅400.3=4×10−60.3=4×10−60.3≈1.33×10−5T
According to Faraday's law of electromagnetic induction, the induced emf (E) in the loop is given by:
E=−A⋅dBdt
Since B is changing due to the changing current, we can express dBdt in terms of dIdt:
dBdt=μ04π⋅2d⋅dIdt
Substituting the values:
dBdt=(4π×10−7)4π⋅20.3⋅(−40)=10−7⋅2⋅(−40)0.3
=−8×10−70.3=−2.67×10−6T/s
E=−0.5⋅(−2.67×10−6)=1.33×10−6V
The average emf induced in the loop is approximately:
E≈1.33×10−6V
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CONCEPTUAL QUESTIONS
22 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - TOUGH & TRICKY PROBLEMS
14 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
A coducting circular loop of area 1mm2 is placed coplanarly with a long, straight wire at a distance of 20 cm from if. The straight wire carries an electric current which changes from 10A to zero is 0.1 s. Find the average emf induced in the loop in 0.1 s.
View SolutionA long solenoid with 1.5 turns per cm has a small loop of area 2.0cm2 placed inside the solenoid normal to its axis. If the current in the solenoid changes steadily from 2.0A to 4.0A in 1.0s. The emf induced in the loop is
View Solution
Knowledge Check
A long straight wire is parallel to one edge of a rectangular loop as shown in figure-5.310. if the current in the long wire varies with time as I=I0e−tr, what will be the induced emf in the loop at t=τ?
Aμ0bIπτIn(d+ad)Bμ0bI2πτIn(d+ad)C2μ0bIπτIn(d+ad)Dμ0bIπτIn(dd+a)20 ampere current is flowing in a long straight wire. The intensity of magnetic field at a distance 10 cm from the wire will be
A4×10−5Wb/mB9×10−5Wb/mC8×10−5Wb/mD6×10−5Wb/mA square conducting loop is placed in the neighbourhood of a coplaner long straight wire carrying a current i.
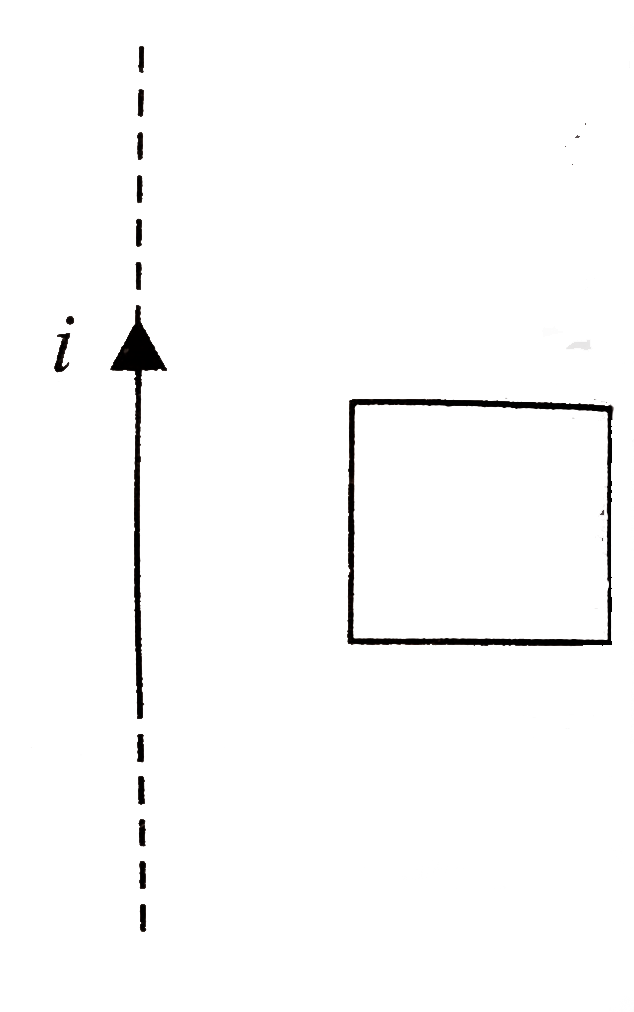Aif didt=0, no current is induced in the loopBif didt>0 , current in the loop is clockwise.Cif didt<0 , current in the loop is anticlockwise.Dif didt>0 , current in the loop is anticlockwise.
A square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is
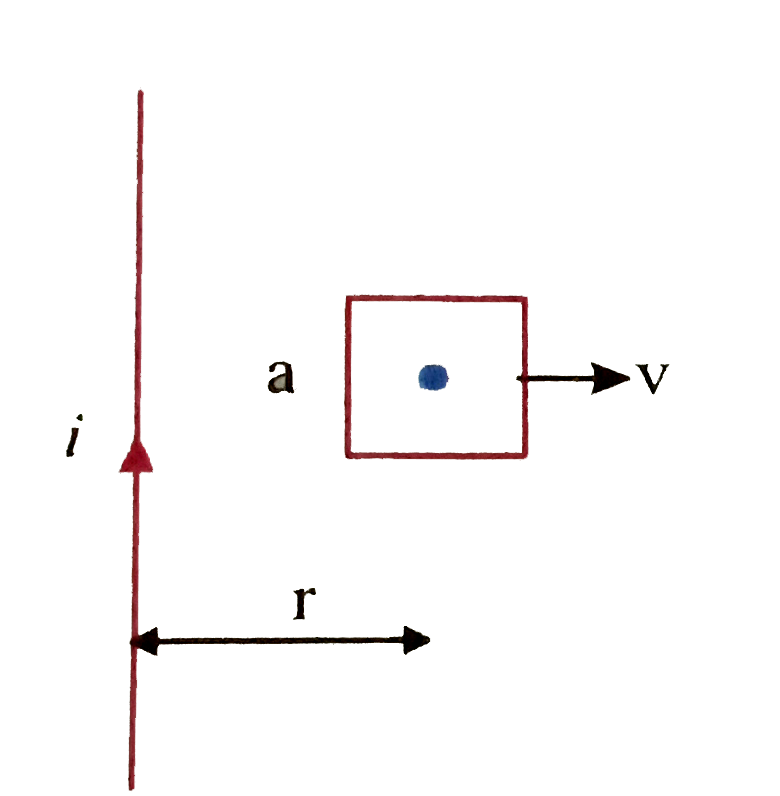
View SolutionA rectangular loop of wire shown below is coplanar with a long wire carrying current I.
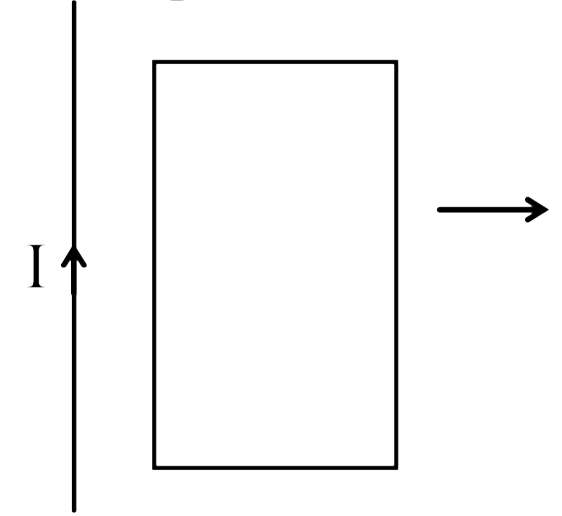The loop is pulled to the right as indicated. What are the directions of the induced current in the loop and the magnetic forces on the left and the right sides of the loop
View SolutionA long, straight wire carries a current. Is Ampere's law
valid for a loop that does not enclose the wire, or that
encloses the wire but is not circular?
View SolutionA square loop is placed near a long current carrying straight wire as shown in the figure . Match the following table
View SolutionFigure shows a conducting loop placed near a long straight wire carrying a current i as shown, if the current increases continuously, find the direction of the induced current in the loop.
View Solution