A 0.5m long metal rod PQ completes the circuit as shown in the figure. The area of the circuit is perpendicular to the magnetic field of flux density 0.15T. If the resistance of the total circuit is 3Ω calculate the force needed to move the rod in the direction as indicated with a constant speed of 2ms−1
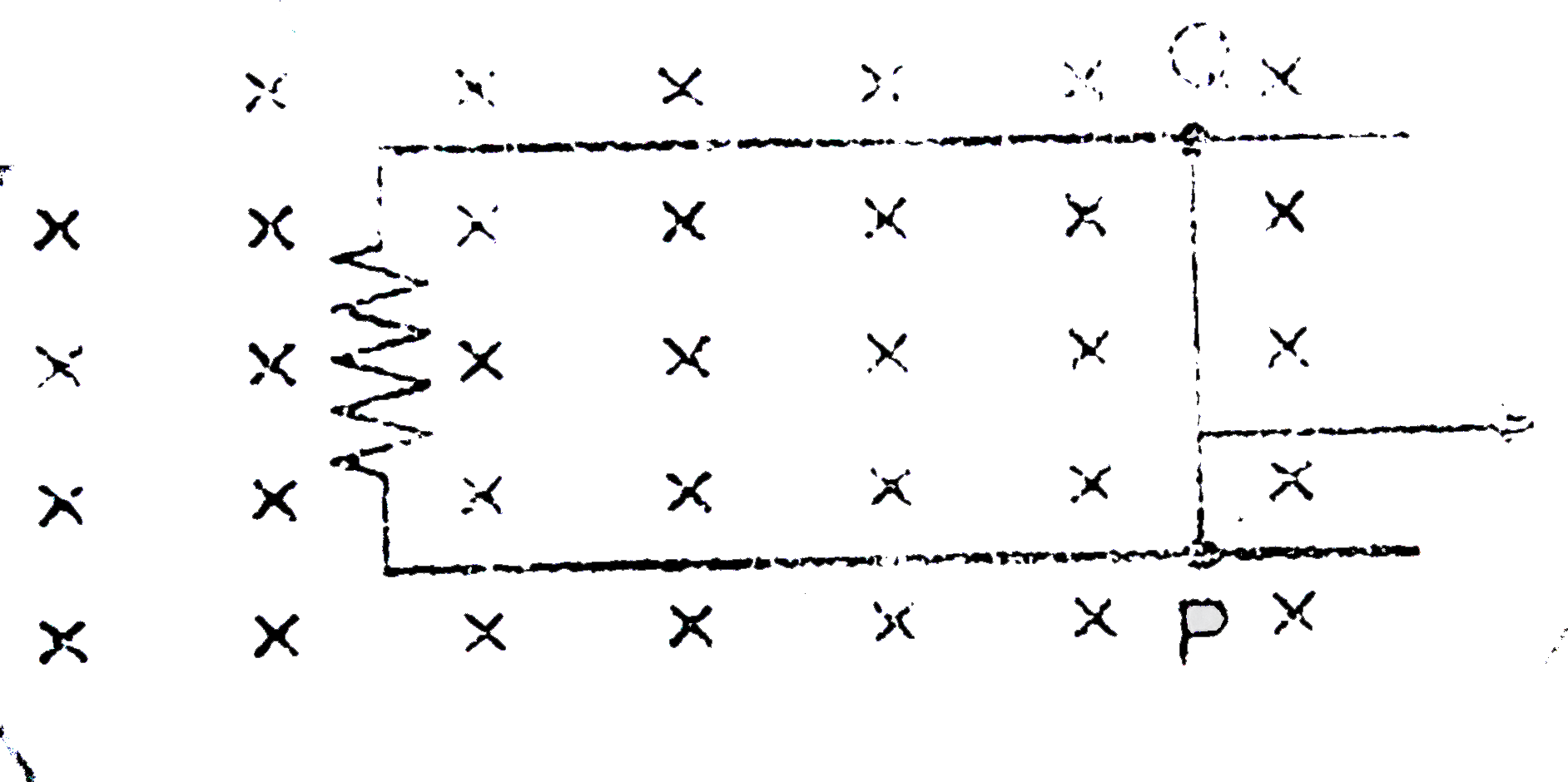
Emf induced across a rod of length l, moving with velocity v in an external magnetic field B is
ε=Blv
Induced current will be
I=εR
where R is the resistance of the circuit=BlvR
Magnitude of force acting on a current carrying conductor of length l, moving in magnetic field is
F=IlBsinθ
Here, θ=90∘
⇒F=IlB=BlvR.lB=B2l2vR
Given, B=0.15 T, l=0.5 m, v=2m/s , R=3Ω
⇒F=(0.15)2×(0.5)2×23=3.75×10−3V
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE PROBLEMS
25 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CONCEPTUAL QUESTIONS
22 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
A 0.5 m long metal rod PQ completes the circuit as shown in the Fig. 6.47. The area of the circuit is perpendicular to the magnetic field of flux density 0.15 T. If the resistance of the total circuit is 3Ω, calculate the force needed to move the rod in the direction as indicated with a constant speed of 2ms−1.
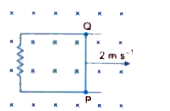
View SolutionAs shown in figure, a metal rod completes the circuit. The circuit area is perpendicular to a magnetic field with B=0.15T. If the resistance of the total circuit is 3Ω, how large a force is needed to move the rod as indicated with a constant speed of 2 m/s?
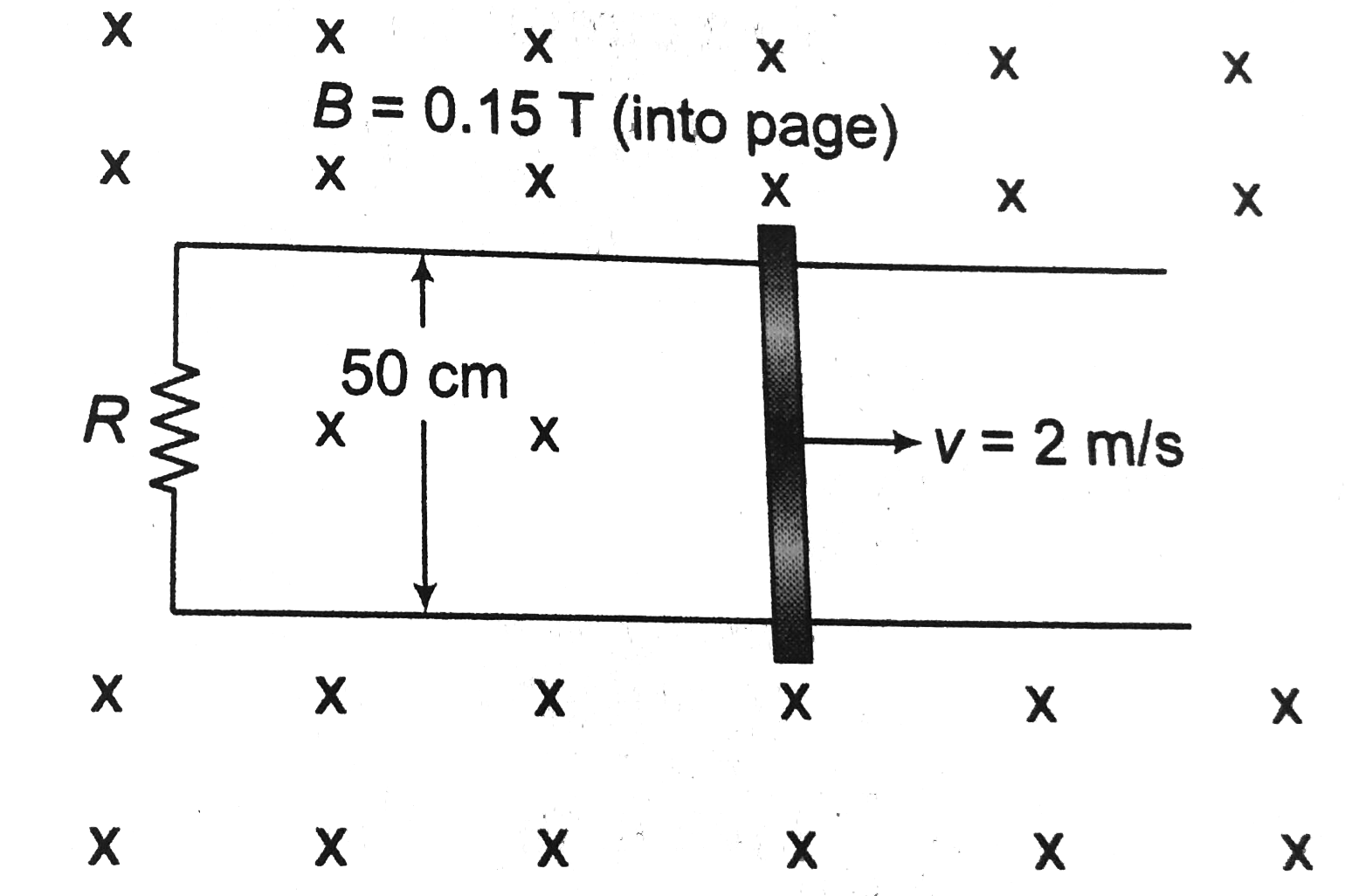
View Solution
Knowledge Check
As shown in figure, a metal rod completes the circuit. The circuit area is perpendicular to a magnetic field with B=0.15T. If the resistance of the total circuit is 3Ω, how large a force is needed to move the rod as indicated with a constant speed of 2 m/s?
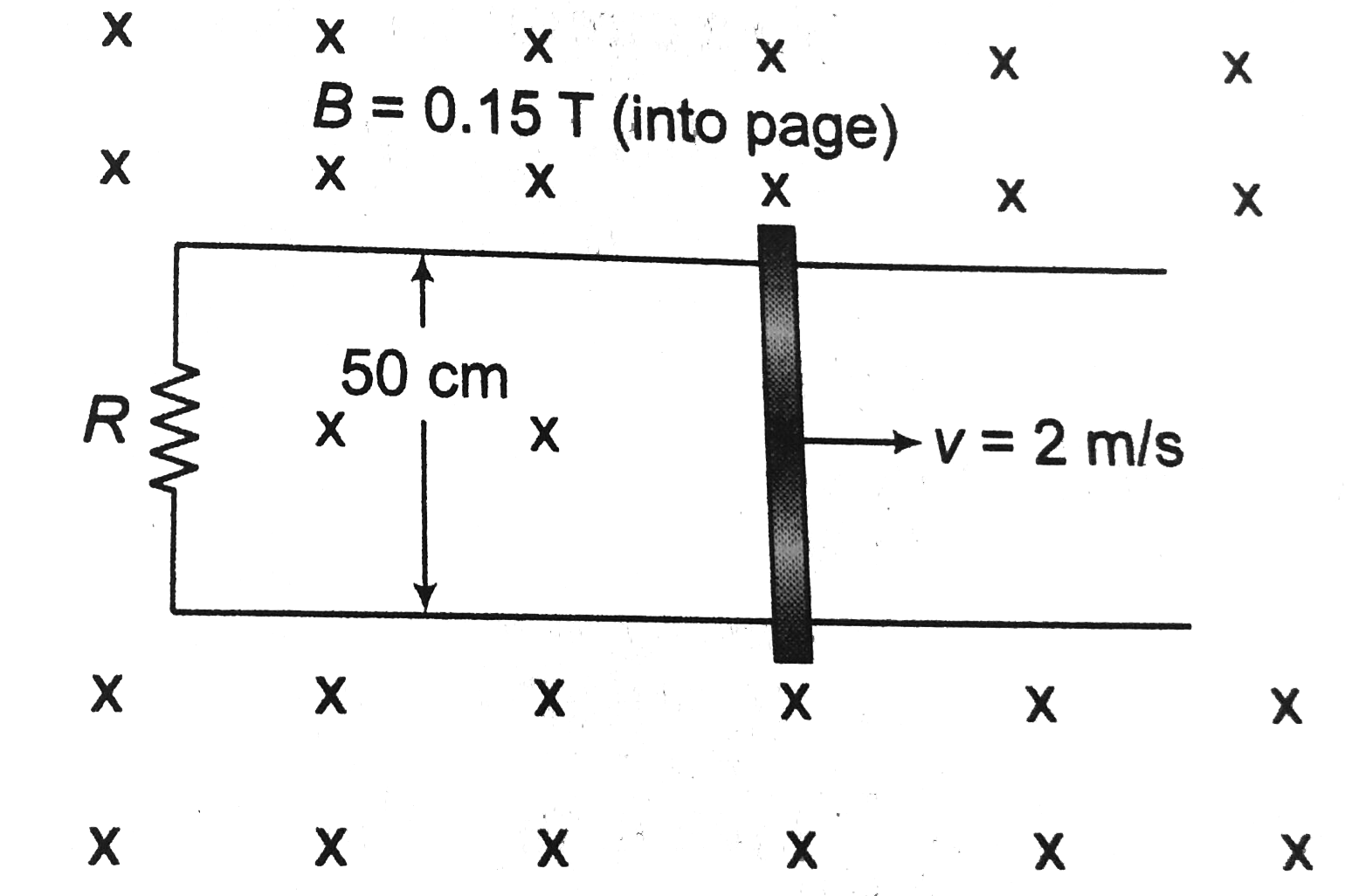 A3.75×10−3NB3.75×10−2NC3.75×102ND3.75×10−4
A3.75×10−3NB3.75×10−2NC3.75×102ND3.75×10−4A metallic rod completes its circuit as shown in the figure. The circuit is normal to a magnetic field of B=0.15 tesla. If the resistances of the rod is 3Ω the force required to move the rod with a constant velocity of 2m/sec is-
 A3.75×10−3NB3.75×10−2NC3.75×102ND3.75×10−4N
A3.75×10−3NB3.75×10−2NC3.75×102ND3.75×10−4NA metallic rod completes its circuit as shown in the figure. The circuit is normal to a magnetic field of B=0.15 tesla. If the resistances of the rod is 3Ω the force required to move the rod with a constant velocity of 2m/sec is-
 A3.75×10−3NB3.75×10−2NC3.75×102ND3.75×10−4N
A3.75×10−3NB3.75×10−2NC3.75×102ND3.75×10−4N
A metal rod of length l cuts across a uniform magnetic field B with a velocity v. If the resistance of the circuit of which the rod forms a part is r, then the force required to move the rod is
View SolutionA wire of length 1m is moving at a speed of 2ms−1 perpendicular to its length and a homogeneous magnetic field of 0.5T. The ends of the wire are joined to a circuit of resistance 6Ω. The rate at which work is being done to keep the wire moving at constant speed is
View SolutionA battery of e mf 10 V and internal resistance 3Ω is connected to a resistor as shown in the figure. If the current in the circuit is 0.5 A . then the resistance of the resistor will be
View SolutionA metal rod of length 2 m is rotating with an angualr velocity of 100rads−1 in plane perpendicular to a uniform magnetic field of 0.3 T. The potential difference between the ends of the rod is
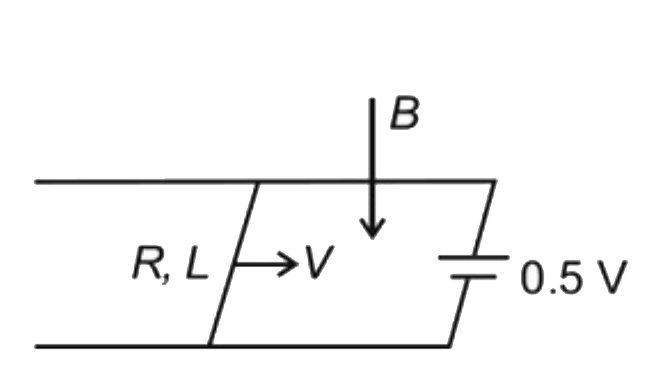
View SolutionThere is a pair of fixed, parallel rails of negligible resistance in a horizontal plane, at a distance of L = 10 cm. The rails are connected, at one of their ends to an ideal battery of EMF 0.5 V, as shown in the figure. The system is placed in a vertically downward and perpendicular magnetic field of magnetic induction B = 1T. A metal rod of resistance R=10Ω is placed perpendicularly on the rails. The rod placed perpendicularly on the rails. The rod and rails are frictionless. The magnitude of force, which is to be exerted on the rod in order to move it with a constant speed of order to move it with a constant speed of 1ms−1 in the direction shown, is
View Solution
