Suppose we want to verify the analogy between electrostatic and magnetostatic by an explicit experiment. Consider the motion of (i) electric dipole →p in an electrostatic field →E and (ii) magnetic dipole →M in a magnetic field →B. Write down a set of conditions on →E, →B, →p, →M so that the two motions are verified to be identical. (Assume identical initial conditions).
Magnitude of the torque acting on an electric dipole of moment p in an electrostatic field →E is given by τ=pEsinθ
Magnitude of the torque acting on a magnetic dipole of moment →M in a magnetic field B is given by
τ.=MBsinθ
Since the motions of the two dipoles are identical, we have:
τ=τ.
pEsinθ=MBsinθ
⇒pE=MB
we know that , E=cB
⇒pcB=MB
→p=→Mc
Topper's Solved these Questions
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:COMPETITION FILE (INTEGER TYPE QUESTIONS)
Explore 7 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Chapter Practice Test
Explore 9 Videos
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:CHAPTER PRACTICE TEST
Explore 13 Videos
Similar Questions
Write the expression for the force →F acting on a charged particle of charge q moving with a velocity →v in the presence of both electric field →E and magnetic field →B . Obtain the condition under which the particle moves underflected through the fields.
View SolutionA charged particle moving with a uniform velocity →v enters a region where uniform electric and magnetic fields →E and →B are present. It passes through the region without any change in its velocity. What can we conclude about the (i) relative direction of →E, →V and →B? (ii) magnetic of →E and →B?
or
Find the condition under which the charged particle moving with different speeds in the presence of electric and magnetic field vectors can be used to select charged particles of a particular speeds.
View Solution
Knowledge Check
Statement A : A proton has spin and magnetic moment just like an electron. But its effect is neglected in magnetism of material.
Statement B : The order of magnitude of difference between the diamagnetic suceptibility of N2(~5×10−9)(STP)andCu(~10−5) is 1.6×10−4
Statement C : Suppose we went to verify the analogy between electrostatic and magnetostatic by an explicit experiment. Consider the motion of (i) electric dipole P in an electrostatic field E and (ii) magnetic dipole M in a magnetic field B. Set of conditions on E,B,p,M so that the two motions are verified to be identical. (Assume identical initial contiditions are (i) P=MC
(ii) PE = MBAA correct B correct C correctBA correct B correct C wrongCA worng B correct C correctDA correct B worng C correctStatement A: A proton has spin and magnetic moment just like an electron. But its effect is neglected in magnetism of materia.
Statement B: The order of magnitude of difference between the diamagnetic susceptibility of N2(~5×10−9)(STP)andCu(~10−5) is 1.6×10−4
Statement C: Suppose we want to verfty the analogy between electrostatic and magnetostatic by an explicit experiment. Consider the motion of (i) electric dipole P in an electrostatic field E and (ii) magnetic dipole M in a magnetic field B . Set of conditons on E,B,p,M so that two motions are verified to be identical. (Assume identical initial contiditions) are (i) P=MC ,(ii) PE=MBAA correct B correct C correctBA correct B correct C wrongCA wrong B correct C correctDA correct B wrong C correct
Write the expression for the force →F, acting on a charged particle of charge q moving with a velocity →v in the pressure of both electric field →E and magnetic field →B. Obtain the condition under which the particle moves undeflected through the fields.
View SolutionRead the following passage and then answer questions (a) to (e) on the basis of your under- standing of the passage and the related studied concepts.
In accordance with Faraday.s law of electromagnetic induction a magnetic field, changing with time, gives rise to an electric field. Again as per Ampere-Maxwell.s law an electric field, changing with time, gives rise to a magnetic field. It means that if we consider a charge oscillating with some frequency, it produces an oscillating electric field in space, which produces an oscillating mag- netic field, which in turn, is a source of oscillating electric field and so on. The oscillating electric and magnetic fields thus regenerate each other and an electromagnetic wave propagates through space. The energy associated with the propagating wave comes at the expense of the energy of the oscillating charge.
Electromagnetic wave propagates through free space as a transverse wave in which →Eand→B are perpendicular to each other as well as perpendicular to the direction of wave propagation. Like other waves electromagnetic waves carry energy and momentum. As electromagnetic waves contains both electric and magnetic fields, it has an electrical energy density μE=12∈0E2 as well as a magnetic energy density μB=B22μ0. Both of these vary with time.
Write an expression for the electric field.
View SolutionRead the following passage and then answer questions (a) to (e) on the basis of your under- standing of the passage and the related studied concepts.
In accordance with Faraday.s law of electromagnetic induction a magnetic field, changing with time, gives rise to an electric field. Again as per Ampere-Maxwell.s law an electric field, changing with time, gives rise to a magnetic field. It means that if we consider a charge oscillating with some frequency, it produces an oscillating electric field in space, which produces an oscillating mag- netic field, which in turn, is a source of oscillating electric field and so on. The oscillating electric and magnetic fields thus regenerate each other and an electromagnetic wave propagates through space. The energy associated with the propagating wave comes at the expense of the energy of the oscillating charge.
Electromagnetic wave propagates through free space as a transverse wave in which →Eand→B are perpendicular to each other as well as perpendicular to the direction of wave propagation. Like other waves electromagnetic waves carry energy and momentum. As electromagnetic waves contains both electric and magnetic fields, it has an electrical energy density μE=12∈0E2 as well as a magnetic energy density μB=B22μ0. Both of these vary with time.
What is the amplitude of electric field vector?
View SolutionRead the following passage and then answer questions (a) to (e) on the basis of your under- standing of the passage and the related studied concepts.
In accordance with Faraday.s law of electromagnetic induction a magnetic field, changing with time, gives rise to an electric field. Again as per Ampere-Maxwell.s law an electric field, changing with time, gives rise to a magnetic field. It means that if we consider a charge oscillating with some frequency, it produces an oscillating electric field in space, which produces an oscillating mag- netic field, which in turn, is a source of oscillating electric field and so on. The oscillating electric and magnetic fields thus regenerate each other and an electromagnetic wave propagates through space. The energy associated with the propagating wave comes at the expense of the energy of the oscillating charge.
Electromagnetic wave propagates through free space as a transverse wave in which →Eand→B are perpendicular to each other as well as perpendicular to the direction of wave propagation. Like other waves electromagnetic waves carry energy and momentum. As electromagnetic waves contains both electric and magnetic fields, it has an electrical energy density μE=12∈0E2 as well as a magnetic energy density μB=B22μ0. Both of these vary with time.
In which direction does the electric field oscillates?
View SolutionRead the following passage and then answer questions (a) to (e) on the basis of your under- standing of the passage and the related studied concepts.
In accordance with Faraday.s law of electromagnetic induction a magnetic field, changing with time, gives rise to an electric field. Again as per Ampere-Maxwell.s law an electric field, changing with time, gives rise to a magnetic field. It means that if we consider a charge oscillating with some frequency, it produces an oscillating electric field in space, which produces an oscillating mag- netic field, which in turn, is a source of oscillating electric field and so on. The oscillating electric and magnetic fields thus regenerate each other and an electromagnetic wave propagates through space. The energy associated with the propagating wave comes at the expense of the energy of the oscillating charge.
Electromagnetic wave propagates through free space as a transverse wave in which →Eand→B are perpendicular to each other as well as perpendicular to the direction of wave propagation. Like other waves electromagnetic waves carry energy and momentum. As electromagnetic waves contains both electric and magnetic fields, it has an electrical energy density μE=12∈0E2 as well as a magnetic energy density μB=B22μ0. Both of these vary with time.
What is the frequency and wavelength of the electromagnetic wave?
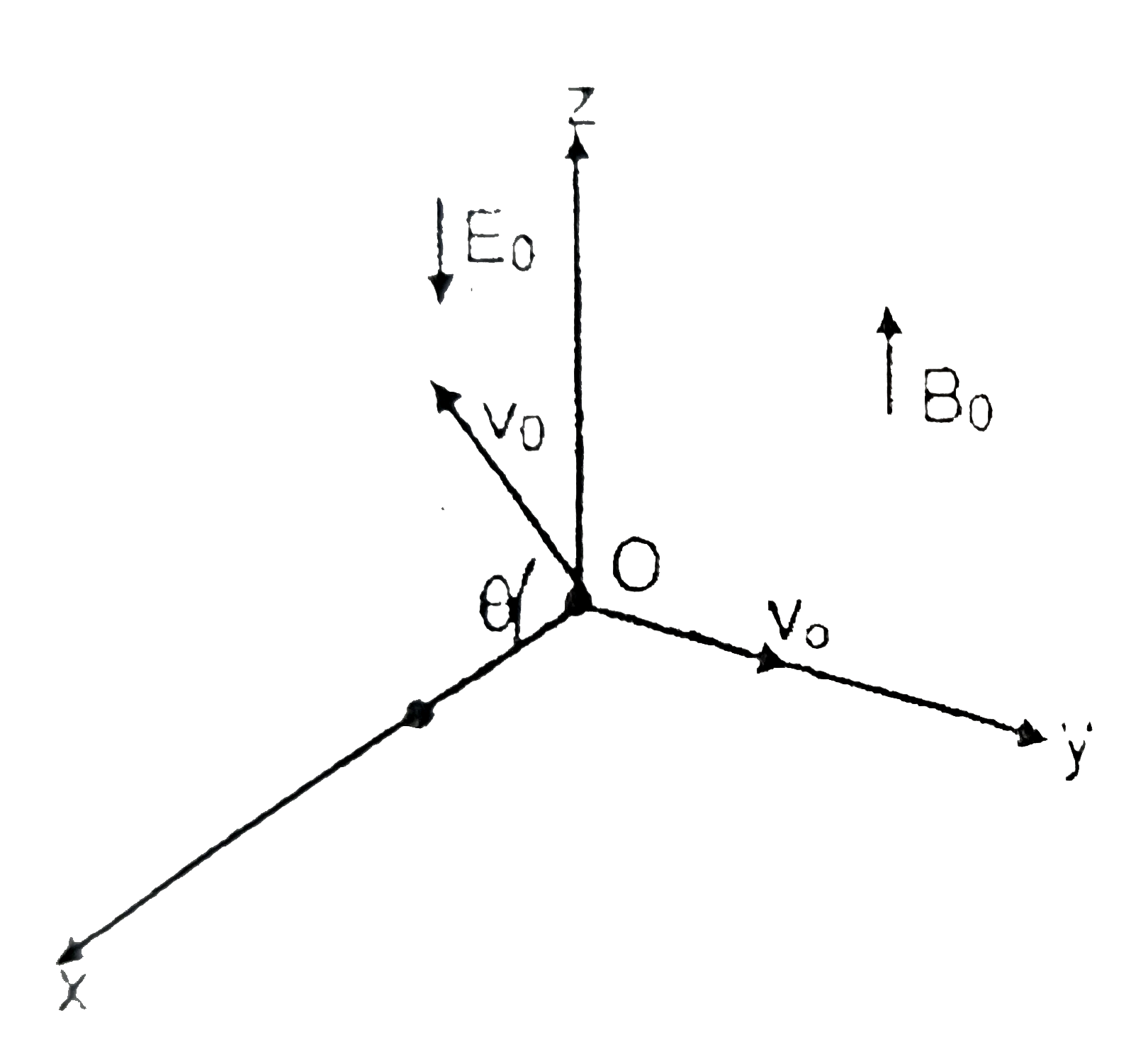
View SolutionA charged point particle having positive charge q, mass m is projected in x−z plane with a speed v0 at an angle θ with the x−axis , while another identical particle is projected simultaneously along the y−axis from the origin (see figure) with an equal speed v0.
An electric field →E=−E0ˆk exists in the x−z plane, while a magnetic field →B=B0ˆk exists in the region y>0 (F0, B0>0). It is observed that both the particles collide after some time. Assume that the space is gravity free.
(i) Find the time after which the particles collide and the coordinates of the point of collision.
(ii) Find the velocity v0 and the angle θ in terms of the other variables.
(iii) What is the maximum value of the z− coordinate of the first particle ?
View Solution

