Three identical parallel plate (air) capacitors C1,C2,C3 have capacitances C each. The space between their plates is now filled with dielectrics as shown. If all the three capacitors still have equal capacitances, obtain the relation between the dielectric constants K,K1,K2,K3andK4.
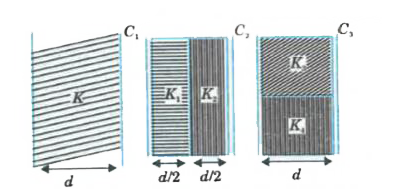
New capacitance of C1,C.=Kε0Ad …(i)
Capacitance of C2
1C.=d2ε0K1A+d2ε0K2A
1C.=d2ε0A(K1+K2K1K2)
C.=ε0d(2K1K2K1+K2) ...(ii)
Capacitance of C3
C.=ε0K3A2d+ε0K4A2d
=ε0Ad+(K3+K42) ...(iii)
From equation (i), (ii) and (iii)
Kε0Ad=ε0Ad(2K1K2K1+K2)
=ε0Ad(K3+K42)
⇒K=2K1K2K1+K2=K3+K42
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Revision Exercises (Numerical Problems)
Explore 25 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Competition file (MULTIPLE CHOICE QUESTIONS based on a given passage/comprehension)
Explore 17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Revision Exercises (Short Answer Questions)
Explore 38 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
Similar Questions
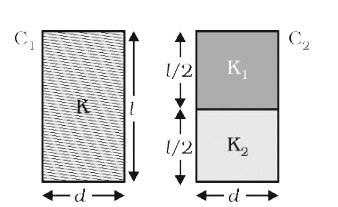
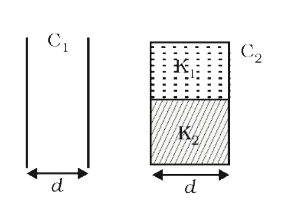
Two identical parallel plate (air) capacitors c1andc2 have capacitances C each. The space between their plates is now filled with dielectrics as shown. If two capacitors still have equal capacitance, obtain the relation betweenn dielectric constants k,k1andk2.
View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View Solution
Knowledge Check
A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
 AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]A paralle plate air capacitor has capacitance C. Now half of the space is fillel with a dielectric material with dielectric constant K as shown in figure . The new capacitance is C . Then
 AC'=C2[1+K]BC'=C[1+K]CC'=C[1+K2]DC'=C[12+K]
AC'=C2[1+K]BC'=C[1+K]CC'=C[1+K2]DC'=C[12+K]A parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
A3CBC3C12 CDC6
Two identical capacitors of plate dimensions: l×b and plate separation d have dielectric slabs filled in between the space of the plates as shown in the figures. if capacitance of both capacitor is same, Obtain the relation between the dielectric constant K,K1andK2.
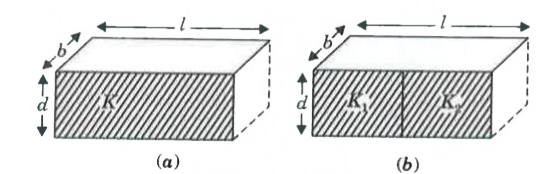
View SolutionTwo identical capacitors of plate dimensions l×b and plate separation 'd' have dielectric slabs filled in between the space of the plates as shown in Fig
Obtain the relation between the dielectric constants K,K1 and K2.
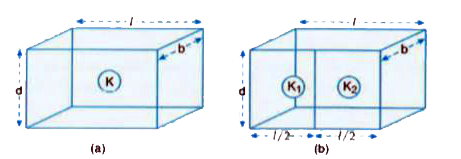
View SolutionYou are given an air filled parallel plate capacitor c1. The space between its plates is now filled with slabs of dielectric constant k1andk2 as shown in c2. Find the capacitances of the capacitor c2 if area of the plates is A distance between the plates is d.
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View Solution

