In ……….. combination, net capacitance of a number of capacitors decreases while in ………….. combination, it increases.
To answer the question regarding the behavior of capacitance in different combinations of capacitors, we can break it down step by step.
Step 1: Understanding Capacitor Combinations
Capacitors can be connected in two main configurations: series and parallel. Each configuration affects the total or net capacitance differently.
Step 2: Series Combination
In a series combination, the total capacitance (C_eq) is calculated using the reciprocal formula:
1Ceq=1C1+1C2+1C3+…+1Cn
This means that the total capacitance is less than the smallest individual capacitor in the series. Therefore, when capacitors are connected in series, the net capacitance decreases.
Step 3: Parallel Combination
In a parallel combination, the total capacitance is simply the sum of the individual capacitances:
Ceq=C1+C2+C3+…+Cn
In this case, the total capacitance is greater than any individual capacitor. Thus, when capacitors are connected in parallel, the net capacitance increases.
Step 4: Conclusion
From the above analysis, we can conclude:
- In series combination, the net capacitance decreases.
- In parallel combination, the net capacitance increases.
Final Answer
In series combination, net capacitance of a number of capacitors decreases while in parallel combination, it increases.
---
Capacitors can be connected in two main configurations: series and parallel. Each configuration affects the total or net capacitance differently.
In a series combination, the total capacitance (C_eq) is calculated using the reciprocal formula:
1Ceq=1C1+1C2+1C3+…+1Cn
This means that the total capacitance is less than the smallest individual capacitor in the series. Therefore, when capacitors are connected in series, the net capacitance decreases.
In a parallel combination, the total capacitance is simply the sum of the individual capacitances:
Ceq=C1+C2+C3+…+Cn
In this case, the total capacitance is greater than any individual capacitor. Thus, when capacitors are connected in parallel, the net capacitance increases.
From the above analysis, we can conclude:
- In series combination, the net capacitance decreases.
- In parallel combination, the net capacitance increases.
In series combination, net capacitance of a number of capacitors decreases while in parallel combination, it increases.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Revision Exercises (Short Answer Questions)38videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Revision Exercises (Long Answer Questions)13videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Revision Exercises (Additional Questions)10videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
The equivalent capacitance of the combination of the capacitors is :
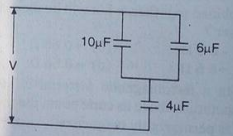 A3.20μFB7.80μFC3.90μFD2.16μF
A3.20μFB7.80μFC3.90μFD2.16μF - Question 2 - Select One
The equivalent capacitance of the combination of the capacitors is :
 A3.20μFB7.80μFC3.90μFD2.16μF
A3.20μFB7.80μFC3.90μFD2.16μF - Question 3 - Select One
For capacitors in series combination, total capacitance C is given by
A1C=1C1+1C2+....BC=C1+C2+....CC=C1C2+C2C3+ . . . .DC+1C1+C2+.....
