How will you connect three capacitors to obtain the maximum charge storage capacity?
To determine how to connect three capacitors to achieve the maximum charge storage capacity, we need to analyze the different configurations: series and parallel.
1. Understanding Capacitance and Charge Storage:
- The charge Q stored in a capacitor is given by the formula:
Q=C×V
- Here, C is the capacitance and V is the potential difference across the capacitor. To maximize Q, we need to maximize C.
2. Capacitor Configurations:
- Capacitors can be connected in two primary configurations: series and parallel.
- In Series: The total or equivalent capacitance Ceq is given by:
1Ceq=1C1+1C2+1C3
- This results in a smaller equivalent capacitance than any individual capacitor, which is not ideal for maximizing charge storage.
3. In Parallel: The total capacitance is simply the sum of the individual capacitances:
Ceq=C1+C2+C3
- This configuration yields the largest equivalent capacitance, as the capacitance values add directly.
4. Conclusion:
- To achieve the maximum charge storage capacity, the three capacitors should be connected in parallel. This configuration maximizes the equivalent capacitance Ceq, and thus maximizes the charge Q stored when a potential difference V is applied.
Final Answer:
Connect all three capacitors in parallel to obtain the maximum charge storage capacity.
---
- The charge Q stored in a capacitor is given by the formula:
Q=C×V
- Here, C is the capacitance and V is the potential difference across the capacitor. To maximize Q, we need to maximize C.
- Capacitors can be connected in two primary configurations: series and parallel.
- In Series: The total or equivalent capacitance Ceq is given by:
1Ceq=1C1+1C2+1C3
- This results in a smaller equivalent capacitance than any individual capacitor, which is not ideal for maximizing charge storage.
Ceq=C1+C2+C3
- This configuration yields the largest equivalent capacitance, as the capacitance values add directly.
- To achieve the maximum charge storage capacity, the three capacitors should be connected in parallel. This configuration maximizes the equivalent capacitance Ceq, and thus maximizes the charge Q stored when a potential difference V is applied.
Connect all three capacitors in parallel to obtain the maximum charge storage capacity.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Revision Exercises (Additional Questions)
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Revision Exercises (Fill in the Blanks)
11 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Higher Order Thinking Skills & Advanced Level (QUESTIONS WITH ANSWERS)
10 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
How would you connectged 8, 12 and 24μF capacitors to obtain (i) minimum capacitance (ii) maximum capacitance ? If a potential difference of 100 volt is applied across the system, what would be the charges on the capacitors in each case?
View SolutionHow will you connected four capacitors, each of capacitance 1μF to obtain a net capacitance of 0.75μF? Draw a diagram to show the combination
View Solution
Knowledge Check
If you are provided three resistances 2Ω,3Ω and 6Ω. How will you connect then so as to obtain the equivalent resistance of 4Ω ?
A B
B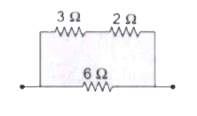 C
C Dnone of these
Dnone of theseIf you are provided three resistance 2Ω,3Ω and 6Ω. How will you connect them so as to obtain the equivalent resistance of 4Ω
A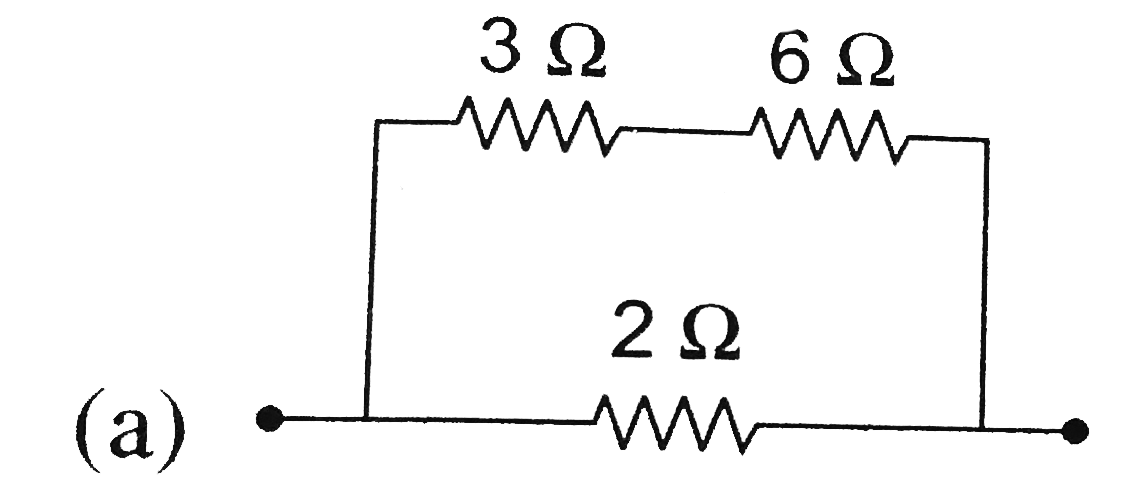 B
B C
C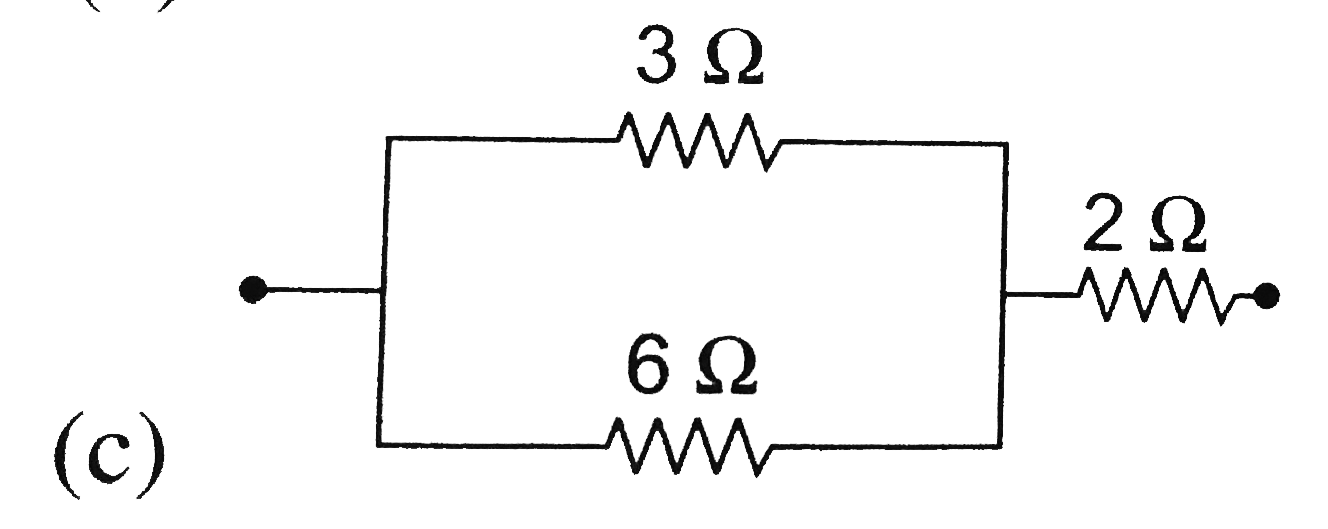 Dnone
DnoneAn uncharged capacitor is connected to a battery. On charging the capacitor
AAll the energy supplied is stored in the capacitorBHalf the energy supplied is stored in the capacitorCThe energy stored depends upon the capacity of the capacitor onlyDThe energy stored depends upon the time for which the capacitor is charged

At t=0 switch S is closed .
(a) After how much time , charge on capacitor is 50% of maximum charge stored on capacitor.
(b) After how much time, energy stored in capacitor is halt of maximum energy stored in capacitor.
View SolutionA 100μF capacitor is charged to 100V. After the charging, battery is disconnected. The capacitor is then connected in parallel to another capacitor. The final voltage is 20V. Calculate cap the capacity of second capacitor.
View SolutionHow will you connect three resistors of 2Ω,3Ω and 6Ω to obtain a total resistance of : (a) 4Ω, and (b) 1Ω?
View SolutionA battery of 10V is connected to a capacitor of capacity 0.lF. The battery is now removed and this capacitor is connected to a second uncharged capacitor. If the charges are distributed equally on these two capacitors, find the total energy stored in the two capacitors. Find the ratio of final energy to initial energy stored in capacitors.
View SolutionIn how many ways one can arrange three idential capacitors taking either one or two or three capacitors together to obtain distinct effective capacitance is
View Solution
