We have two metal plates of surface area 1m2 to construct an air parallel plate capacitor. A potential difference of 210 V is to be applied across the capacitor. The dielectric strength of air is 1 and electric field between the plates is 3×106V/m. What can be the minimum separation between two plates? If the capacitor is constructed accordingly then how much charge it will hold when connected across a 210 V supply?
To solve the problem step by step, we will first find the minimum separation between the plates of the capacitor and then calculate the charge it can hold when connected to a 210 V supply.
Step 1: Calculate Minimum Separation Between Plates
The electric field (E) between the plates of a parallel plate capacitor is given by the formula:
E=Vd
Where:
- E = electric field (in V/m)
- V = potential difference (in V)
- d = separation between the plates (in m)
We can rearrange this formula to find the separation d:
d=VE
Given:
- V=210V
- E=3×106V/m
Substituting the values into the formula:
d=210V3×106V/m
Calculating d:
d=2103×106=7×10−5m
Thus, the minimum separation between the plates is:
d=7×10−5m(or 70 micrometers)
Step 2: Calculate Charge Stored in the Capacitor
The charge Q stored in a capacitor is given by the formula:
Q=C×V
Where:
- C = capacitance (in F)
- V = potential difference (in V)
The capacitance C for a parallel plate capacitor is given by:
C=Aϵ0d
Where:
- A = area of the plates (in m²)
- ϵ0 = permittivity of free space (8.85×10−12F/m)
- d = separation between the plates (in m)
Given:
- A=1m2
- d=7×10−5m
Now substituting the values into the capacitance formula:
C=1m2×8.85×10−12F/m7×10−5m
Calculating C:
C=8.85×10−127×10−5≈1.264×10−7F
Now, substituting C and V into the charge formula:
Q=C×V=1.264×10−7F×210V
Calculating Q:
Q≈2.655×10−5C
To convert this to microcoulombs:
Q≈26.55μC
Final Answers:
1. Minimum separation between the plates: 7×10−5m (or 70 micrometers).
2. Charge stored in the capacitor: 26.55μC.
---
- E = electric field (in V/m)
- V = potential difference (in V)
- d = separation between the plates (in m)
- V=210V
- E=3×106V/m
- C = capacitance (in F)
- V = potential difference (in V)
- A = area of the plates (in m²)
- ϵ0 = permittivity of free space (8.85×10−12F/m)
- d = separation between the plates (in m)
- A=1m2
- d=7×10−5m
1. Minimum separation between the plates: 7×10−5m (or 70 micrometers).
2. Charge stored in the capacitor: 26.55μC.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Revision Exercises (Very Short Answer Questions)
Explore 56 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Revision Exercises (Additional Questions)
Explore 10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:NCERT FILE Solved (Exemplar Problems) (Short Answer Type Questions)
Explore 5 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
Similar Questions
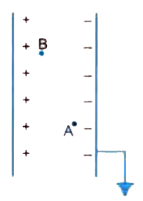
In a parallel plate capacitor the potential difference of 100 V is manitianed between the plates. If distance between the plates be 5mm, what will be the electric field at points A and B ?
View SolutionA potential difference of 250 Volt is applied across the plate of a capacitor of 10 pF. Calculate the charge on the plates of the capacitor.
View Solution
Knowledge Check
Plates of a parallel plate capacitor, having a potential difference 100 V applied across them, carry a surface charge density of 50 nC cm−2. Spacing between the plates is
A329μmB259μmC177μmD125μmIn a parallel plate capacitor, the distance between the plates is d and potential difference across the plate is V. Energy stored per unit volume between the plates of capacitor is
AQ22V2B12ε0V2d2C12V2ε0d2D12ε0V2dFigure shows a parallel plate capacitor with plate area A and plate separation d. A potential difference is being applied between the plates. The battery is then disconnected and a dielectric slab of dielectric constant K is placed in between the plates of the capacitor as shown.

The electric field in the dielectric slab isAVKdBKVdCVdDKVt
A parallel plate capacitor of plate area A and plates separation distance d is charged by applying a potential V0 between the plates. The dielectric constant of the medium between the plates is K. What is the uniform electric field E between the plates of the capacitor ?
View SolutionA parallel plate air capacitor is made using two square plates each of side 0.2 m, spaced 1 cm apart. It is connected to a 50V battery.
What is the electric field between the plates ?
View SolutionFor an isolated parallel plate capacitor of capacitance C and potential difference V, what will be change in (i) charge on the plates (ii) potential difference across the plates (iii) electric field between the plates (iv) energy stored in the capacitor, when the distance between the plates is increased ?
View SolutionThe plates of a parallel-plate capacitor in vacuum are 5.00mm apart and 2.00m2 in area. A potential difference of 10,000V is applied across the capacitor. Compute
(a) the capacitance
(b) the charge on each plate, and
(c) the magnitude of the electric field in the space between them.
View SolutionWhat happens to the stored electric potential energy and the electric field between the plates of a charged isolated parallel plate capacitor when the plate separation is increased?
View Solution

