Two small identical blocks of mass 10 g carrying the same charge of magnitude 0.2 μC are kept at a separation of 0.1 m on a rough table . If both the blocks stay in equilibrium using limiting friction from the surface then calculate the coefficient of friction between the block and the table.
To solve the problem, we need to determine the coefficient of friction between the blocks and the table. Here’s a step-by-step solution:
Step 1: Identify the Given Data
- Mass of each block, m=10g=0.01kg
- Charge on each block, q=0.2μC=0.2×10−6C
- Separation between the blocks, r=0.1m
- Gravitational acceleration, g=10m/s2
Step 2: Calculate the Electric Force Between the Blocks
The electric force Fe between two charges can be calculated using Coulomb's law:
Fe=kq1q2r2
where k is Coulomb's constant, k=9×109N m2/C2.
Substituting the values:
Fe=9×109(0.2×10−6)2(0.1)2
Calculating (0.2×10−6)2=0.04×10−12=4×10−14:
Fe=9×1094×10−140.01=9×109×4×10−12=36×10−3=0.036N
Step 3: Calculate the Weight of Each Block
The weight W of each block is given by:
W=mg=0.01×10=0.1N
Step 4: Set Up the Equation for Limiting Friction
In equilibrium, the electric force is balanced by the frictional force F:
Fe=F
The frictional force can be expressed as:
F=μN
where N is the normal force. Since the blocks are on a horizontal table, the normal force N is equal to the weight of the block:
N=W=0.1N
Thus, we have:
Fe=μW
Substituting the known values:
0.036=μ×0.1
Step 5: Solve for the Coefficient of Friction μ
Rearranging the equation gives:
μ=0.0360.1=0.36
Final Answer
The coefficient of friction between the block and the table is:
μ=0.36
- Mass of each block, m=10g=0.01kg
- Charge on each block, q=0.2μC=0.2×10−6C
- Separation between the blocks, r=0.1m
- Gravitational acceleration, g=10m/s2
The electric force Fe between two charges can be calculated using Coulomb's law:
Fe=kq1q2r2
where k is Coulomb's constant, k=9×109N m2/C2.
Fe=9×109(0.2×10−6)2(0.1)2
Calculating (0.2×10−6)2=0.04×10−12=4×10−14:
Fe=9×1094×10−140.01=9×109×4×10−12=36×10−3=0.036N
The weight W of each block is given by:
W=mg=0.01×10=0.1N
In equilibrium, the electric force is balanced by the frictional force F:
Fe=F
The frictional force can be expressed as:
F=μN
where N is the normal force. Since the blocks are on a horizontal table, the normal force N is equal to the weight of the block:
N=W=0.1N
Thus, we have:
Fe=μW
Substituting the known values:
0.036=μ×0.1
Rearranging the equation gives:
μ=0.0360.1=0.36
The coefficient of friction between the block and the table is:
μ=0.36
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Practice Problems
Explore 88 Videos
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Conceptual Questions
Explore 51 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
- ELECTROMAGNETIC INDUCTIONBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 14 Videos
Similar Questions
A block of weight 10 N lies on a rough table. It just moves when a force of 7N is applied on it. Calculate the coefficient of limiting friction between the block and the table.
View SolutionA wooden block of mass m resting on a rough horizontal table is pulled by a force F as shown in the figure. If μ is the coefficient of friction between block and table, its acceleration will be
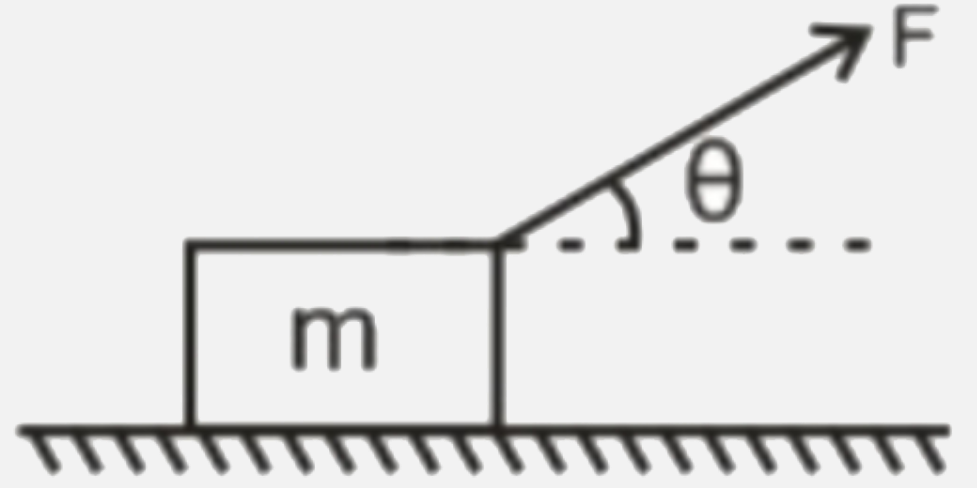
View Solution
Knowledge Check
A block slides with a velocity of 10 m/s on a rough horizontal surface. It comes to rest after covering a distance of 50 metre. If g is 10m/s2, then the coefficient of dynamic friction between the block and the surface is
A0.1B1C10D5A block of mass M is being pulley along horizontal surface .The coefficient of friction the block and the surface is μ If another block of mass M/2 is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
AμB3μ2C2μD5μ2A block of mass 4 kg is resting on a horizontal table and a force of 10 N is applied on it in the horizontal direction. The coefficient of kinetic friction between the block and the table is 0.1. The work done in √20 s
ABy the applied force is 150 JBBy the frictional force is 60 JCBy the applied force and the net force are 150 J and 90 J respectivelyDAll are correct
A rectangular block is kept on a rough horizontal surface and given some initial velocity. The coefficient of friction between the block and the surface is constant. The block will topple
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionFind the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
View SolutionA block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pully at the edge of the table and from its other end another block B of mass m2 is suspended. The coefficient of kinetic friction between the block and the table is H. When the block A is sliding on the table, the tension in the string is
View SolutionA block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View Solution