Consider two solid spheres P and Q each of density 8gmcm−3 and diameters 1cm and 0.5cm, respectively. Sphere P is dropped into a liquid of density 0.8gmcm−3 and viscosity η=3 poiseulles. Sphere Q is dropped into a liquid of density 1.6gmcm−3 and viscosity η=2 poiseulles. The ratio of the terminal velocities of P and Q is
When buoyant force plus air resistance becomes equal to weight of sphere then terminal speed is attained. If V represents terminal speed then it can be shown that Vrα(p−σ)r2η
p=density of sphere, and σ= density of medium.
VPTVQT=(8−0.8)×12×23x(8−16)×0.52=3
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (Matching Type Questions )
2 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
A hollow sphere of external and internal diameter 4 cm and 2 cm, respectively, floats in a liquid of density 3.5 g cm−3. The level of the liquid coincides with the center of the sphere. Calculate the density of the material of the sphere.
View SolutionA copper ball of density 8.6gcm−3 and 1 cm in diameter is immersed in oil of density 0.8gcm−3. What is the charge on the ball, if it remains just suspended in oil in electric field of intensity 3600V/m acting in the upward direction ?
View Solution
Knowledge Check
A sphere of radius R and density ρ1 is dropped in a liquid of density σ. Its terminal velocity is v1. If another sphere of radius R and density ρ2 is dropped in the same liquid, its terminal velocity will be:
A(ρ2−σρ1−σ)v1B(ρ1−σρ1−σ)v1C(ρ1ρ2)v1D(ρ2ρ1)v1Two spheres P and Q of the same colour and having radii 4 cm and 2 cm are kept at 127∘Cand527∘C respectively. The ratio of the energies radiated by P and Q
A1:2B1:4C3:1D4:1Two spheres P and Q of equal radii have densities ρ1 and ρ2, respectively. The spheres are connected by a massless string and placed in liquids L1 and L2 of densities σ1 and σ2 and viscosities η1 and η2, respectively. They float in equilibrium with the sphere P in L1 and sphere Q in L2 and the string being taut(see figure). If sphere P alone in L2 has terminal velocity →Vp and Q alone in L1 has terminal velocity →VQ, then
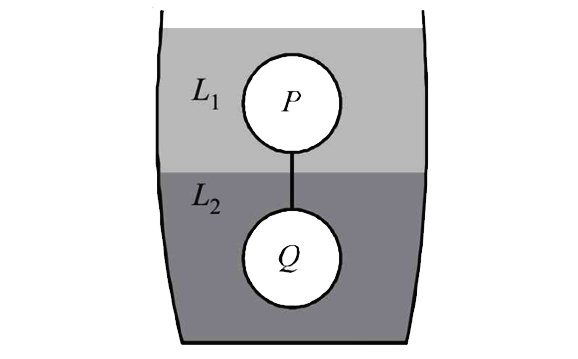 A(a) ∣∣→VP∣∣∣∣→VQ∣∣=η1η2B(b) ∣∣→VP∣∣∣∣→VQ∣∣=η2η1C(c) →VP.→VQ>0D(d) →V.→VQ<0
A(a) ∣∣→VP∣∣∣∣→VQ∣∣=η1η2B(b) ∣∣→VP∣∣∣∣→VQ∣∣=η2η1C(c) →VP.→VQ>0D(d) →V.→VQ<0
A physics student took a solid sphere of density 2 g cm−3 and radius 3.5 cm and applied a force on the sphere. If an acceleration fo 1.5 cms−2 is produced in it, find the amount of force applied on it.
View SolutionWith what terminal velocity will an air bubble of density 1kgm−3 and 0.6 mm diameter rise in a liquid of viscosity 0.15Nsm−2 and specific gravity 0.9 ? What is the terminal velocity of the same bubble in water of η=1×10−3Nsm−2 ?
View SolutionA hollow sphere of inner radius 8.0 cm and outer radius 9.0 cm floats half-submerged in a liquid of density 820 kg/m3. (a) What is the mass of the sphere? (b) Calculate the density of the material of which the sphere is made.
View SolutionStatement-1 : When two speres of same size but of different densities are dropped in a fluid, sphere of greater density will have greater terminal velocity.
And
Statement-2 : Greater the density and viscosity of the fluid, lesser will be the terminal velocity.
View SolutionIf an oil drop of density 0.95×103kg/m3 and radius 10−4 cm is falling in air whose density is 1.3kg/m3 and coefficient of viscosity is 18×10−6kg/(m−s). Calculate the terminal speed of the drop.
View Solution
