Question

(a) Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be $2M{R}^2/5,whereM$ is the mass of the sphere and $R$ is the radius of the sphere.
(b) Given the moment of inertia of a disc of mass $M$ and radius $R$ about any of its diameters to be $\frac{1}{4}M{R}^2$, find the moment of inertia about an axis normal to the disc passing through a point on its edge.

Explanation

Given moment of inertia of a sphere about a diameter `I_(AB)=(2)/(5) MR^(2)`

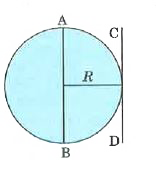
To find moment of inertia of the sphere about a tangent CD, we use parallel axes theorem.
`:.` Moment of inertia of the sphere about the tangent CD is given by
`I_(T)=I_(AB)+MR^(2)=(2)/(5)MR^(2)+MR^(2)`
`I_(T)=(7)/(5)MR^(2)`
(b) Given moment of inertia of circular dise about diameter,
`I_(d)=(1)/(4) MR^(2)`

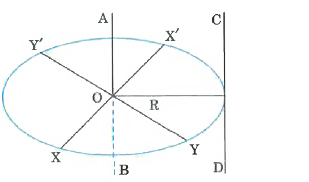
To find the moment of inertia of the disc about an axis normal to the disc eand passing through the centre, we use perpendicular axis theorem.
`I_(d)=` moment of inertia about any of the two dimaeters XX and YY
Using perpendicular axis theorem,
MI of the disc about AB,
`I_(AB)=I_(d)+I_(d)=(1)/(4)MR^(2)+(1)/(4)MR^(2)`
`I_(AB)=(1)/(2)MR^(2)`
To find MI of the disc about a tangent perpendicular to its plane and passing through a point on its edge, we use parallel axis theorem
`I_(T)=I_(AB)+MR^(2)`
`I_(T)=(1)/(2)MR^(2)+MR^(2)=(3)/(2)MR^(2)`