Calculate the percentage error in value of R is .
To calculate the percentage error in the value of resistance R, we can use the formula for resistance given by Ohm's Law:
R=VI
where V is the voltage and I is the current. The errors in the measurements of V and I will contribute to the error in R.
Step 1: Identify the values and their uncertainties
- Given voltage V=50±5 V
- Given current I=5±1 A
Step 2: Calculate the relative error in voltage V
The relative error in V can be calculated as:
ΔVV=550=0.1
Step 3: Calculate the relative error in current I
The relative error in I can be calculated as:
ΔII=15=0.2
Step 4: Calculate the total relative error in resistance R
The total relative error in R is the sum of the relative errors in V and I:
ΔRR=ΔVV+ΔII=0.1+0.2=0.3
Step 5: Convert the total relative error to percentage
To find the percentage error, we multiply the total relative error by 100:
Percentage error=ΔRR×100=0.3×100=30%
Conclusion
The percentage error in the value of resistance R is ±30%.
---
- Given voltage V=50±5 V
- Given current I=5±1 A
The relative error in V can be calculated as:
The relative error in I can be calculated as:
The total relative error in R is the sum of the relative errors in V and I:
To find the percentage error, we multiply the total relative error by 100:
The percentage error in the value of resistance R is ±30%.
Topper's Solved these Questions
- UNITS AND MEASUREMENTBook:MODERN PUBLICATIONChapter:UNITS AND MEASUREMENTExercise:CONCEPTUAL QUESTIONS
Explore 27 Videos
- UNITS AND MEASUREMENTBook:MODERN PUBLICATIONChapter:UNITS AND MEASUREMENTExercise:TOUGH AND TRICKY PROBLEMS
Explore 6 Videos
- UNITS AND MEASUREMENTBook:MODERN PUBLICATIONChapter:UNITS AND MEASUREMENTExercise:CHAPTER PRACTICE TEST
Explore 15 Videos
- THERMAL PROPERTIES OF MATTERBook:MODERN PUBLICATIONChapter:THERMAL PROPERTIES OF MATTERExercise:CHAPTER PRACTICE TEST
Explore 15 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
The resistance R of a conductor is defind as the ratio of the potential difference applied across it to the current flowing through ti . If V = (100±5)V and I = (5+0.1) A , what is the percentage error in R ?
View SolutionIn Ohm's law experimental verification, the reading of voltage and resistance are (120±5)V and (2±0.1)Ω respectively. What is the percentage error in the value of current obtained?
View Solution
Knowledge Check
An experiment measures quantities a, b and c and X is calculated from X=ab2/c3. If the percentage error in a, b and c are ±1%,±3%and±2% respectively, the percentage error in X will be-
A±13%B±7%C±4%D±1%The radius of a ball is (5.2±0.2) cm. The percentage error in the volume of the ball is (approximately).
A0.11B0.04C0.07D0.09The value of resistance of an unknown resistor is calculated using the formula R=V/I where V and I are the readings of the voltmeter and the ammeter, respectivley. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RVandRG,respectively) are finite and nonzero.
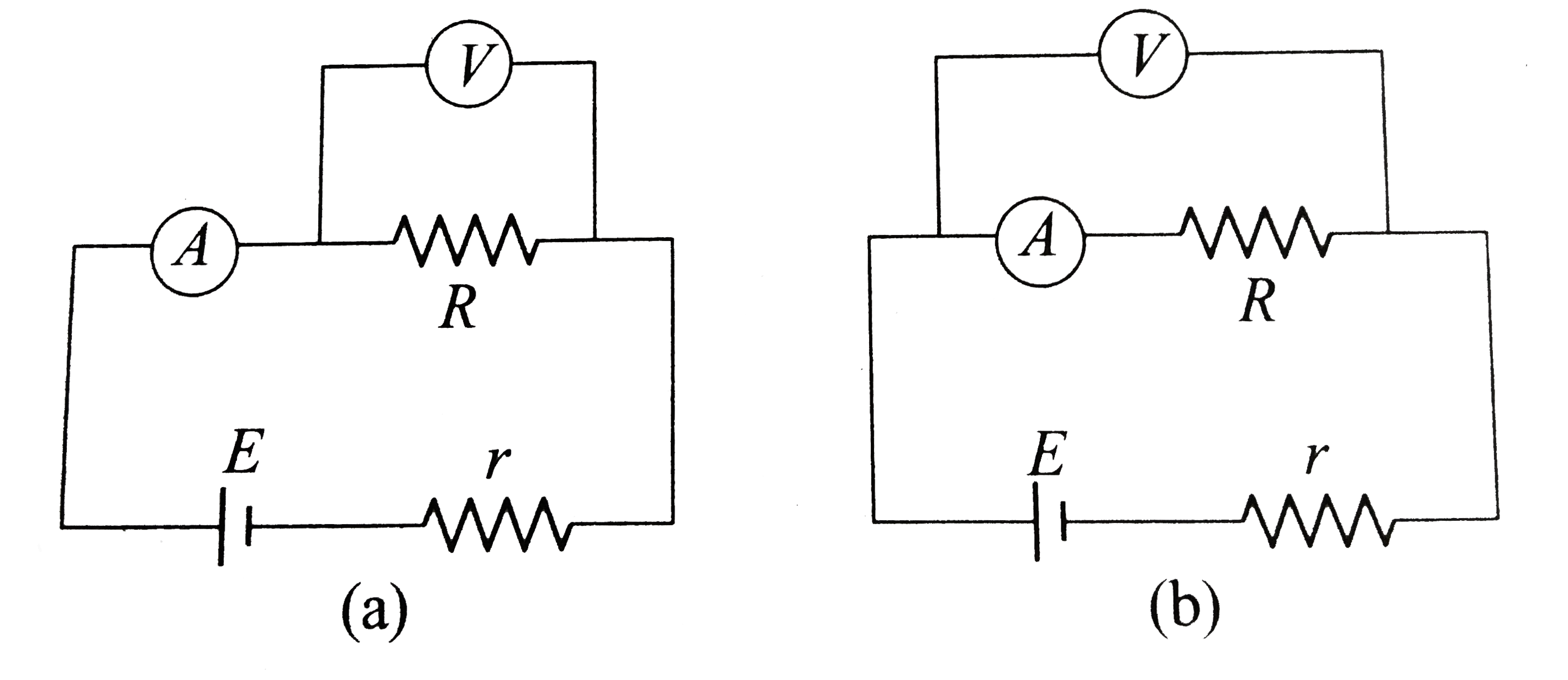 ,
,
Let RAandRB be the calculated values in the two cases A and B , respectively.
If the resistance of voltmeter is RV=1kΩ and the percentage error in the measurement of R (the value of R is nearly 10Ω)isAzero in both casesBnonzero but equal in both casesCmore in circuit ADmore in circuit B
The measures of the length and breadth of a rectangle are (30±3%) and (10.0±0.5%) m. Calcualte the percentage error in the perimeter of the rectangle.
[Hint : Perimeter = (length + breadth).]
View SolutionThe measure of the radius of a sphere is (3.00±2%) cm. Calculate the percentage error in volume and area. Also calculate the absolute error in volume and surface area.
View SolutionResistance value of an unknown resistor is calculated using the formula R=VI where V and I be the readings of the voltmeter and the ammeter respectively. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RvandRGrespectively ) are finite and non zero.

Let RvandRG be the calculated values in the two cases A and B respectively.
If the resistance of voltmeter is Rv=1kΩ and that of ammeter is RG=1Ω the magnitude of the percentage error in the measurement of R (the value of R is nearly 10Ω ) is:
View SolutionFoci are (±3,0) and vertices (±5,0)
View SolutionThe voltage measured across resistance is V=(50±0.1)V and current isI=(10±0.2). Find error in resistance
View Solution

