Centripetal force (F) on a body of mass (m) moving with uniform speed (v) in a circle of radius (r ) depends upon m, v and r. The formula for the centripetal force using theory of dimensons.

Video Solution

Text Solution

Verified by Experts

Let $F = k m^{a} v^{b} r^{c} = m^{a} v^{b} r^{c} [= 1]$
Then $M^{1} L^{1} T^{- 2} = {[M]}^{a} {[L T^{- 1}]}^{b} {[L]}^{c}$
$= [M^{a} L^{b + c} T^{- b}]$
Comparing the exponents of M, L and T on both sides, we get
$a = 1, b + c = 1$
$b = 2$
$\Rightarrow c = 1 - b = 1 - 2 = - 1$
$F = \frac{m v^{2}}{r}$
This is the required expression.

|

Updated on:21/07/2023

Class 11 PHYSICS DIMENSION AND MEASUREMENT

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Figure shows a body of mass m moving with a uniform speed v along a circle of radius r . The change in velocity in going from A to B is

A $v \sqrt{2}$
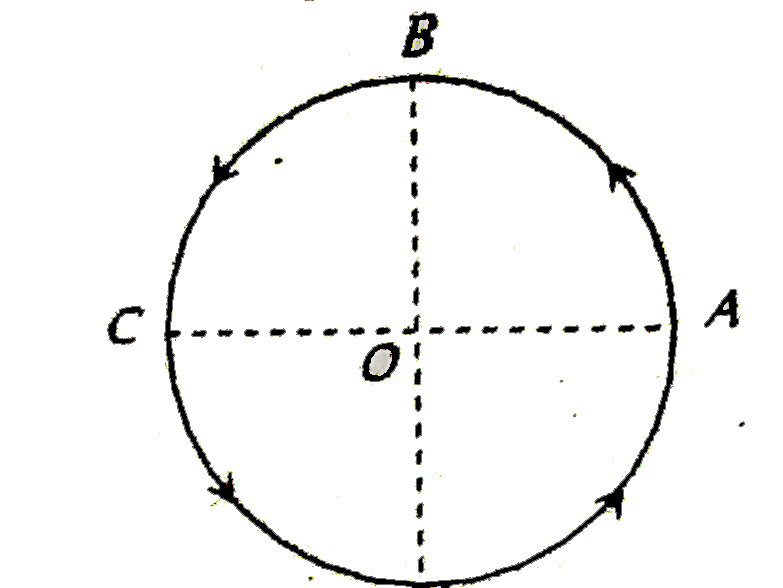B $v / \sqrt{2}$
Cv
DZero
Question 2 - Select One
If a body is moving with a uniform speed v in a circle of radius 'r', then the angular acceleration of the body will be
A $v / r$
B $\frac{v^{2}}{r}$ along the radius and away from the centre
C $\frac{v^{2}}{r}$ along radius and toward centre
Dzero
Question 3 - Select One
The magnitude of the centripetal force acting on a body of mass m executing uniform motion in a circle of radius r with speed v is
Amvr
B $m v^{2} / r$
C $v / r^{2} m$
D $v / r m$

MODERN PUBLICATION-UNITS AND MEASUREMENT-CHAPTER PRACTICE TEST

Home
Ask Doubt
Profile