For a reversible process at T = 300K, the volume is increased from Vi=1L to Vf=10L. Calculate ΔH if the process is isothermal -
11.47 kJ
4.98 kJ
0
−11.47kJ
The correct Answer is:C
To calculate the change in enthalpy (ΔH) for a reversible isothermal process at a temperature of T = 300 K, where the volume is increased from Vi = 1 L to Vf = 10 L, we can follow these steps:
1. Understand the Concept of Enthalpy (ΔH):
The change in enthalpy (ΔH) for a system can be expressed as:
ΔH=ΔU+Δ(PV)
where ΔU is the change in internal energy and Δ(PV) is the change in the product of pressure and volume.
2. Use the Ideal Gas Law:
For an ideal gas, the relationship between pressure (P), volume (V), and temperature (T) is given by:
PV=nRT
where n is the number of moles, R is the ideal gas constant, and T is the temperature in Kelvin.
3. Determine Δ(PV):
Since we are considering a reversible isothermal process, we can express Δ(PV) as:
Δ(PV)=nR(Tf−Ti)
However, since the process is isothermal, the temperature does not change (T_f = T_i = T). Therefore, ΔT = 0, and thus:
Δ(PV)=0
4. Calculate ΔU for an Isothermal Process:
For an ideal gas undergoing an isothermal process, the change in internal energy (ΔU) is also zero because internal energy for an ideal gas depends only on temperature. Since there is no change in temperature:
ΔU=0
5. Substitute Values into the Enthalpy Equation:
Now substituting the values of ΔU and Δ(PV) into the enthalpy equation:
ΔH=ΔU+Δ(PV)=0+0=0
6. Conclusion:
Therefore, the change in enthalpy (ΔH) for this isothermal process is:
ΔH=0
Final Answer:
ΔH=0 kJ
The change in enthalpy (ΔH) for a system can be expressed as:
ΔH=ΔU+Δ(PV)
where ΔU is the change in internal energy and Δ(PV) is the change in the product of pressure and volume.
For an ideal gas, the relationship between pressure (P), volume (V), and temperature (T) is given by:
PV=nRT
where n is the number of moles, R is the ideal gas constant, and T is the temperature in Kelvin.
Since we are considering a reversible isothermal process, we can express Δ(PV) as:
Δ(PV)=nR(Tf−Ti)
However, since the process is isothermal, the temperature does not change (T_f = T_i = T). Therefore, ΔT = 0, and thus:
Δ(PV)=0
For an ideal gas undergoing an isothermal process, the change in internal energy (ΔU) is also zero because internal energy for an ideal gas depends only on temperature. Since there is no change in temperature:
ΔU=0
Now substituting the values of ΔU and Δ(PV) into the enthalpy equation:
ΔH=ΔU+Δ(PV)=0+0=0
Therefore, the change in enthalpy (ΔH) for this isothermal process is:
ΔH=0
ΔH=0 kJ
Topper's Solved these Questions
- THERMODYNAMICS Book:ALLENChapter:THERMODYNAMICS Exercise:EXERCISE -2
Explore 100 Videos
- THERMODYNAMICS Book:ALLENChapter:THERMODYNAMICS Exercise:EXERCISE -3
Explore 108 Videos
- THERMODYNAMICS Book:ALLENChapter:THERMODYNAMICS Exercise:EXERCISE -1A
Explore 41 Videos
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:CHEMISTRY
Explore 19 Videos
- Thermodynamics And Thermo ChemistryBook:ALLENChapter:Thermodynamics And Thermo ChemistryExercise:All Questions
Explore 39 Videos
Similar Questions
If 1.0 kcal of heat is added to 1.2 L of O2 in a cyclinder of constant pressure of 1 atm , the volume increase to 1.5 L . Calculate ΔU and ΔHof the process.
View Solution10g of argon gas is cmpressed isothermally and reversibly at a temperature of 27∘C from 10L to 5L. Calculate enthalpy change (ΔH) for this process R=2.0calK−1mol−1. log102=0.30
Atomic mass of Ar=40
View Solution
Knowledge Check
One mole of an ideal monatomic gas undergoes the following four reversible processes :
Step1 : It is first compressed adiabatically from volume V1 to 1m3.
Step 2 : then expanded isothermally to volume 10 m3.
Step 3 : then expanded adiabatically to volume V3.
Step 4 : then compressed isothermally to volume V1.
If the efficiency of the above cycle is 3/4 then V1 is,A2m3B4m3C6m3D8m310 g of argon gas is compressed isothermally and reversibly at a temperature of 27∘C from 10 L to 5 L. Calculate q and ΔH for this process. Atomic wt. of Ar=40.
A+103.99 cal, 0B+39.99 cal, 3 JC−39.99 cal, 3 JD−103.99 cal, 0Two moles of an ideal gas undergo the following process :
(a) a reversible isobaric expansion from (P atm, VL) to (P atm , 2VL).
(b) a reversible isochoric change of state from (P atm , 2V,L) to (P/2 atm, 2VL)
(c) a reversible isothermal compression from (P/2 atm, 2VL) to (P atm, VL).
Sketch with labels each of the processes on the same P−V diagram.A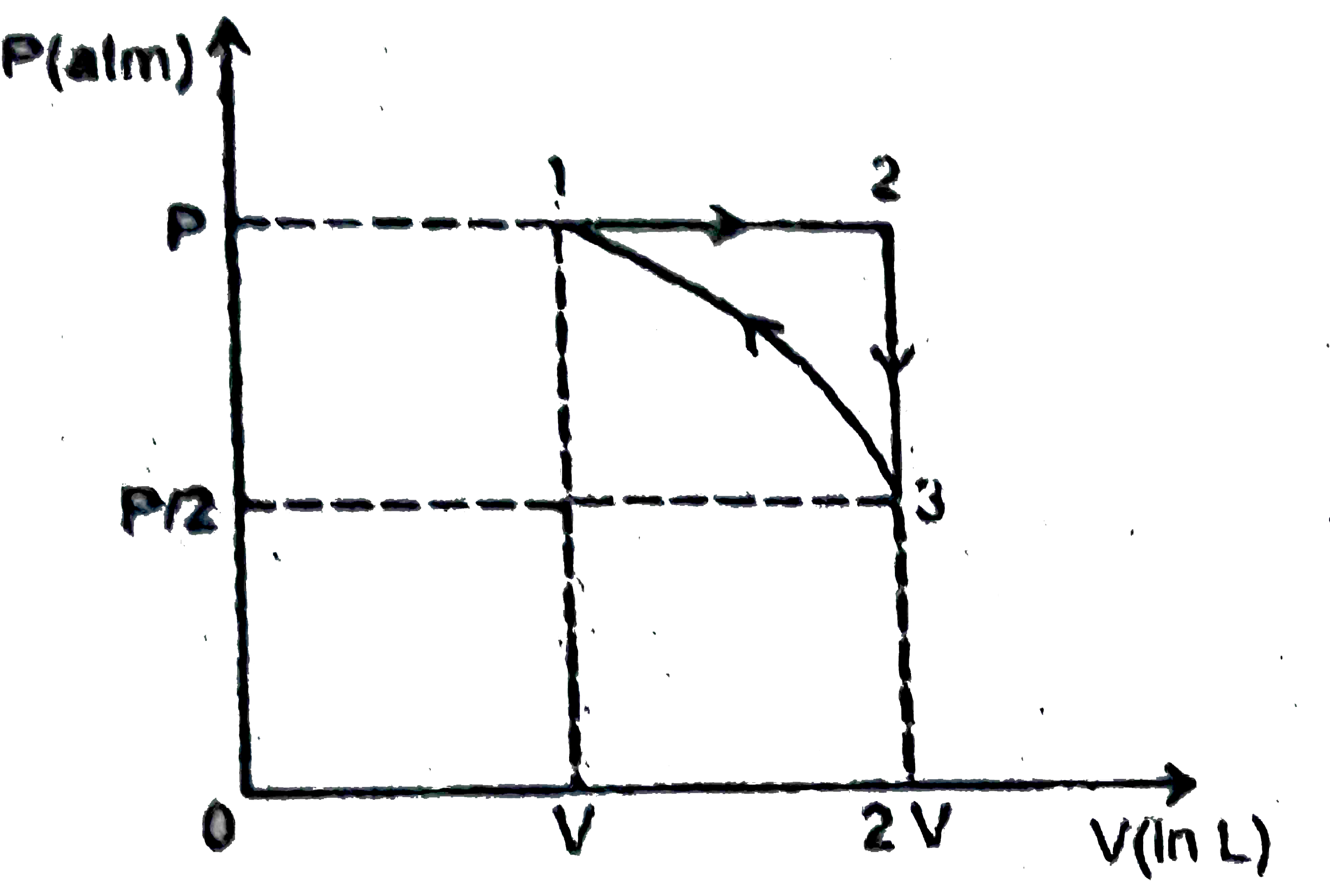 B
B C
C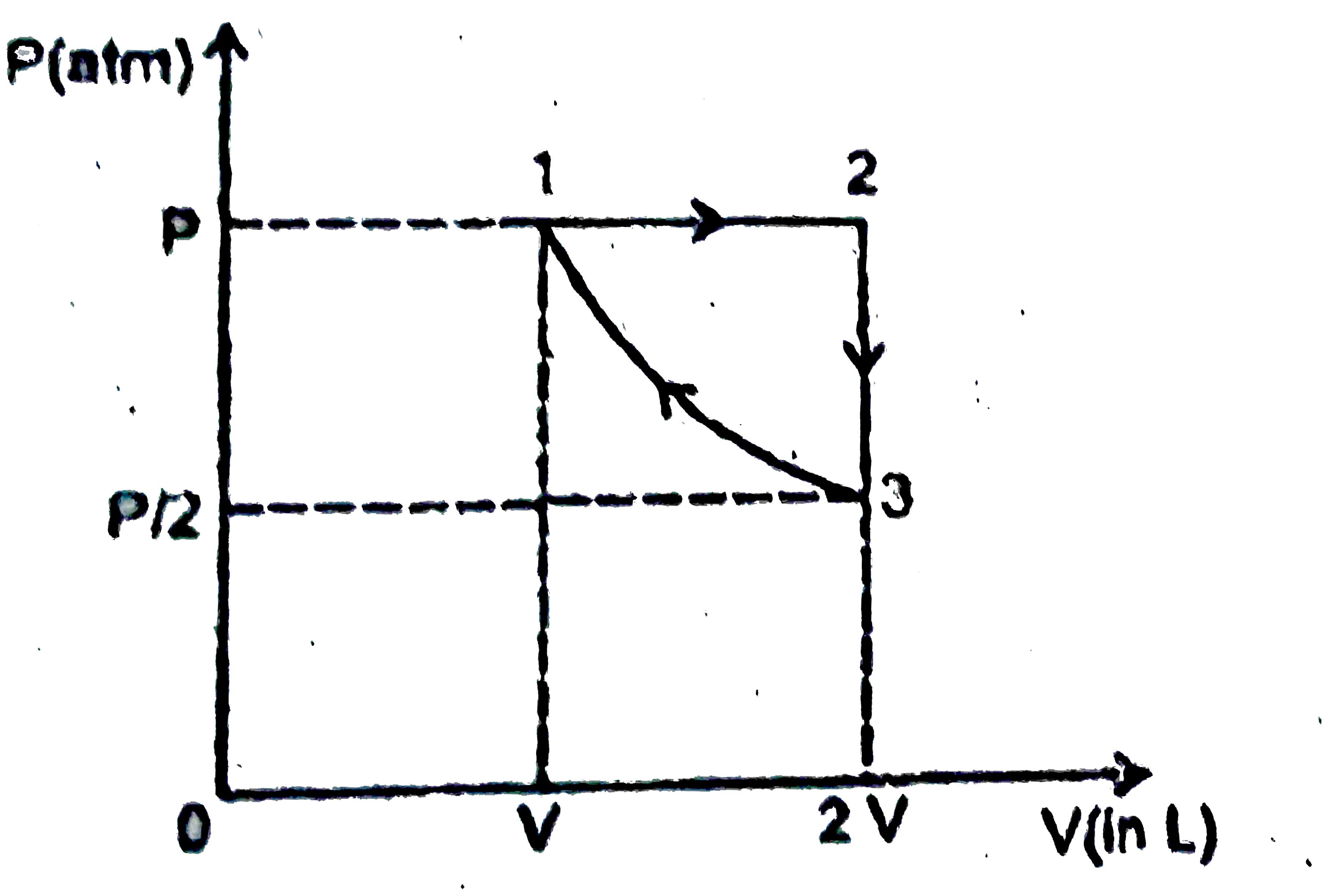 D
D
10g of argon gas is compressed isothermally and reversibly at a temperature of 27∘C from 10L to 5L. Calculate q,w,ΔU, and ΔH for this process. R=2.0calK−1mol−1,log102=0.30. Atomic weight of Ar=40.
View Solution10 g of argon gas is compressed isothermally and reversibly at a temperature of 27∘C from 10 L of 5L. Calculate q, W, ΔU and Δ H for this process. R = 2.0 cal K−1mol−1,log102 = 0.30, Atomic wt. of Ar = 40.
View Solution10g of argon gas is compressed isothermally and reversibly at a temperature of 27∘C from 10L to 5L. Calculate q,w,D≤taU, and ΔH for this process. R=2.0calK−1mol−1,log102=0.30. Atomic weight of Ar=40.
View SolutionA sample of 4 mole He is originally confined in 20L at 270K and then undergoes adiabatic expansion against a constant pressure of untill the volume has increased by factor of 3. Calculate ΔT during process:
View Solution10 grams of argon gas is compressed isothermally and reversibly at a temperature of 27∘C from 10L to 5L .Calculate the work done for this process in multiple of 102 calories.
View Solution

