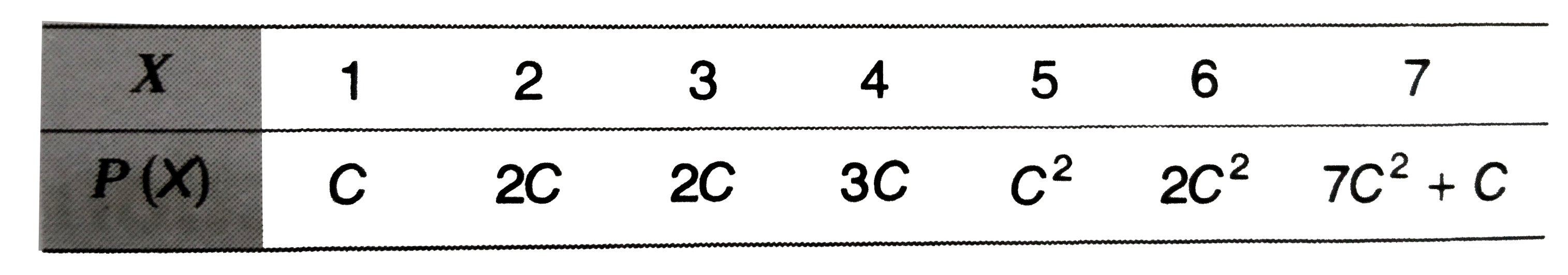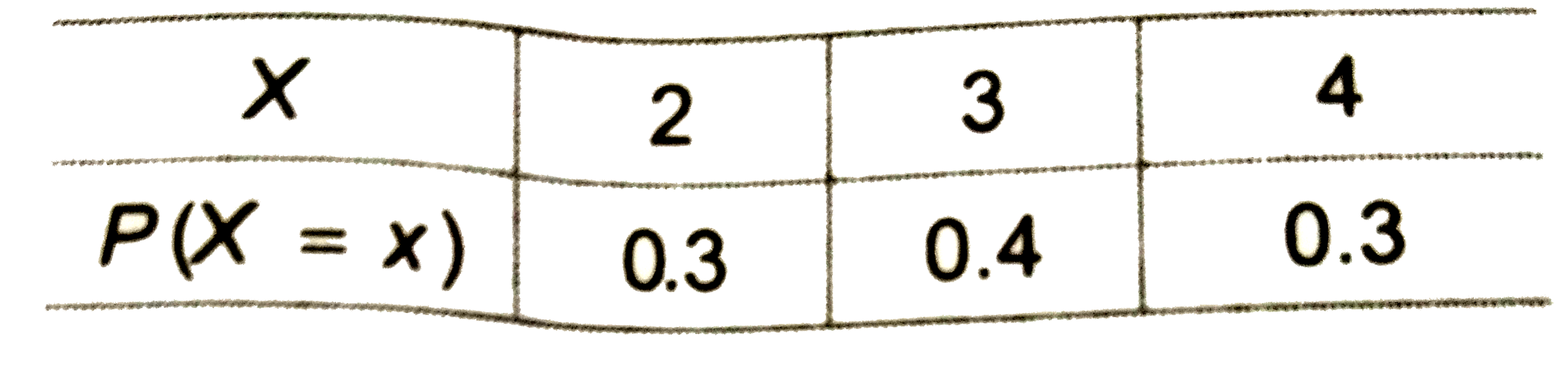A discrete random variable 'X' has mean equal to 3 and variance equal to 2. Assuming that the underlying distribution of 'X' is binomial, find the distribution and hence obtain :
(i) P(X = 0)
(ii) Draw a histogram for the distribution.
The correct Answer is:(23+13)9 (i) (23)9
To solve the problem, we need to find the parameters of the binomial distribution given the mean and variance of the random variable X.
Step 1: Identify the Mean and Variance Formulas
In a binomial distribution, the mean (μ) and variance (σ2) are given by:
- Mean: μ=np
- Variance: σ2=npq
Where:
- n = number of trials
- p = probability of success
- q = probability of failure (where q=1−p)
Step 2: Set Up the Equations
From the problem, we know:
- Mean (μ) = 3
- Variance (σ2) = 2
This gives us two equations:
1. np=3 (1)
2. npq=2 (2)
Step 3: Substitute q in Terms of p
Since q=1−p, we can substitute q in equation (2):
np(1−p)=2
Substituting np=3 from equation (1):
3(1−p)=2
Step 4: Solve for p
Now, we can solve for p:
3−3p=23p=1p=13
Step 5: Find q
Now that we have p, we can find q:
q=1−p=1−13=23
Step 6: Find n
Now, we can substitute p back into equation (1) to find n:
n⋅13=3n=3⋅3=9
Step 7: Summary of Parameters
We have found:
- n=9
- p=13
- q=23
Thus, the binomial distribution is X∼B(9,13).
Step 8: Calculate P(X=0)
Using the binomial probability formula:
P(X=r)=(nr)prqn−r
For X=0:
P(X=0)=(90)(13)0(23)9=1⋅1⋅(23)9=(23)9
Calculating (23)9:
=2939=51219683
Step 9: Draw a Histogram
To draw a histogram for the distribution, we would plot the probabilities P(X=r) for r=0,1,2,…,9.
1. Calculate P(X=r) for r=0,1,2,…,9 using the binomial formula.
2. Use a graphing tool or software to plot the values.
In a binomial distribution, the mean (μ) and variance (σ2) are given by:
- Mean: μ=np
- Variance: σ2=npq
- n = number of trials
- p = probability of success
- q = probability of failure (where q=1−p)
From the problem, we know:
- Mean (μ) = 3
- Variance (σ2) = 2
1. np=3 (1)
2. npq=2 (2)
Since q=1−p, we can substitute q in equation (2):
np(1−p)=2
Substituting np=3 from equation (1):
3(1−p)=2
Now, we can solve for p:
3−3p=23p=1p=13
Now that we have p, we can find q:
q=1−p=1−13=23
Now, we can substitute p back into equation (1) to find n:
n⋅13=3n=3⋅3=9
We have found:
- n=9
- p=13
- q=23
Using the binomial probability formula:
P(X=r)=(nr)prqn−r
For X=0:
P(X=0)=(90)(13)0(23)9=1⋅1⋅(23)9=(23)9
=2939=51219683
To draw a histogram for the distribution, we would plot the probabilities P(X=r) for r=0,1,2,…,9.
2. Use a graphing tool or software to plot the values.
Topper's Solved these Questions
- PROBABILITYBook:MODERN PUBLICATIONChapter:PROBABILITYExercise:Objective Type Question (A. Multiple Choice Questions)
Explore 50 Videos
- PROBABILITYBook:MODERN PUBLICATIONChapter:PROBABILITYExercise:Objective Type Question (B. Fill in the Blanks)
Explore 15 Videos
- PROBABILITYBook:MODERN PUBLICATIONChapter:PROBABILITYExercise:EXERCISE 13 (g) (LATQ)
Explore 21 Videos
- MATRICESBook:MODERN PUBLICATIONChapter:MATRICESExercise:CHAPTER TEST (3)
Explore 12 Videos
- RELATIONS AND FUNCTIONSBook:MODERN PUBLICATIONChapter:RELATIONS AND FUNCTIONSExercise:CHAPTER TEST (1)
Explore 12 Videos
Similar Questions
Knowledge Check
A discrete random variable X has the following probability distribution

The value of C and the mean of the distribution areA110and3.66B1/20and2.66C1/15and1.33DNone of theseA discrete random variable X has the following probability distribution

The value of C and the mean of the distribution areA110 and 3.66B120 and 2.66C115 and 1.33DNone of theseA random variable X follows Binomial distribution with mean α and variance β. Then,
A0<α<βB0<β<αCα<0<βDβ<0<α
If X follow a binomial distribution with mean 4 and variance 2 find P(X≥5)
View SolutionDiscrete random variable || Mean & variable OF random variable || Binomial probability distribution
View SolutionIf X follows a binomial distribution with mean 3 and variance (3/2) find
(i)P(X≥1)(ii)P(X≤5)
View SolutionA random variable X follows binomial distribution with mean α and variance β. Then,
View SolutionA random variable X has the following probability distribution

Then the variance of this distribution is
View Solution