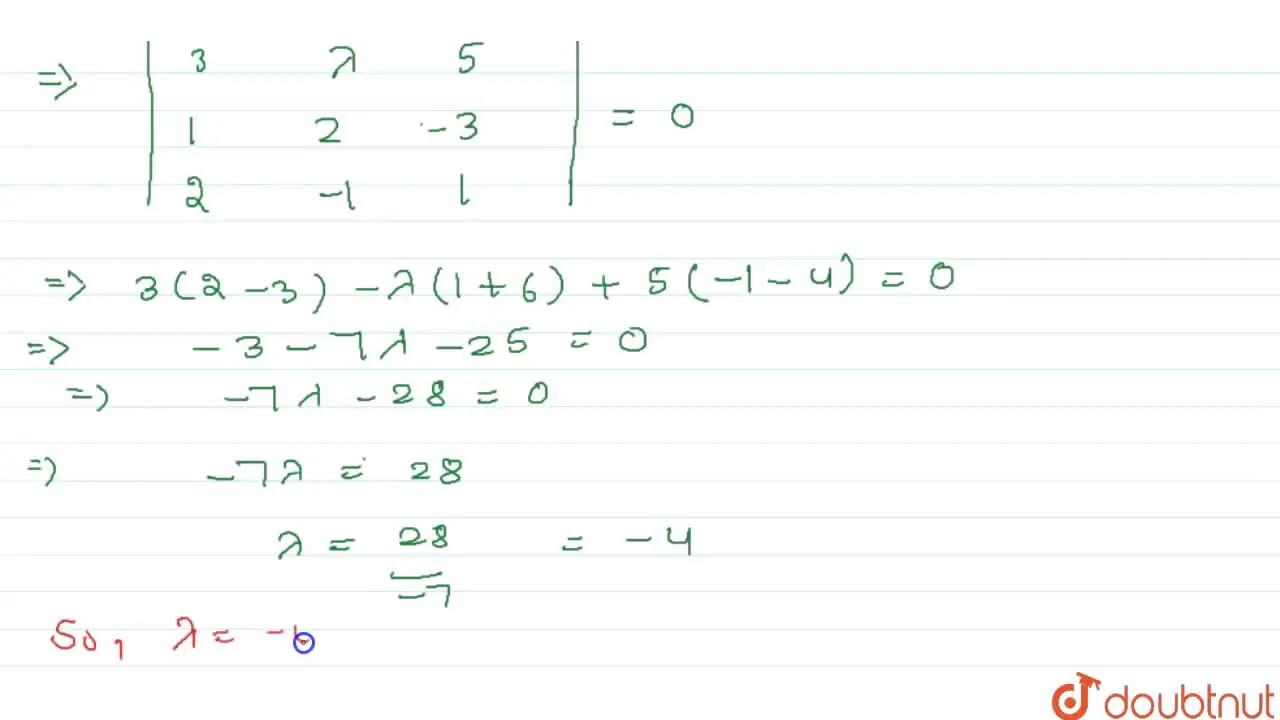Find the value of 'λ' such that vectors : 3ˆi+λˆj+5ˆk,ˆi+2ˆj−3ˆk and 2ˆi−ˆj+ˆk are coplanar.
The correct Answer is:λ=−4
Step by step video, text & image solution for Find the value of 'lambda' such that vectors : 3hat(i)+lambda hat(j)+5hat(k), hat(i)+2hat(j)-3hat(k) and 2hat(i)-hat(j)+hat(k) are coplanar. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
Find the value of 'λ' such that the vectors : 3ˆi+λˆj+5ˆk,ˆi+2ˆj−3ˆk and 2ˆi−ˆj+ˆk are coplanar.
View SolutionThe value of 'λ' such that the vectors :
3ˆi+λˆj+5ˆk,ˆi+2ˆj−3ˆk and 2ˆi−ˆj+ˆk are coplanar is __________.View SolutionWhat is the value of λ for which the vectors ˆi−ˆj+ˆk,2ˆi+ˆj−ˆkandλˆi−ˆj+λ(k) are coplanar
View SolutionWhat is the value of λ for which the vectors ˆi−ˆj+ˆk,2ˆi+ˆj−ˆkandλˆi−ˆj+λˆk are co-planar?
View SolutionWhat is the value of m, if the vector 2ˆi−ˆj+ˆk,ˆi+2ˆj−3ˆkand3ˆi+mˆj+5ˆk are coplanar?
View SolutionShow that the vectors
ˆi−3ˆj+4ˆk,2ˆi−ˆj+2ˆkand4ˆi−7ˆj+10ˆk are coplanar.View SolutionFind 'λ' if the vectors :
ˆi−ˆj+ˆk,3ˆi+ˆj+2ˆk and ˆi+λˆj−3ˆk are coplanar.View SolutionShow that the vectors ˆi−ˆj−6ˆk,ˆi−3ˆj+4ˆkand2ˆi−5ˆj+3ˆk are coplanar.
View SolutionFind the value of λ so that the vectors
→a=2ˆi−3ˆj+ˆk,→b=ˆi+2ˆj−3ˆkand→c=ˆj+λˆk are coplanar.View SolutionIf the vectors ˆi−2ˆj+ˆk,aˆi+5ˆj−3ˆkand5ˆi−9ˆj+4ˆk are coplanar, then the value of a is
View Solution