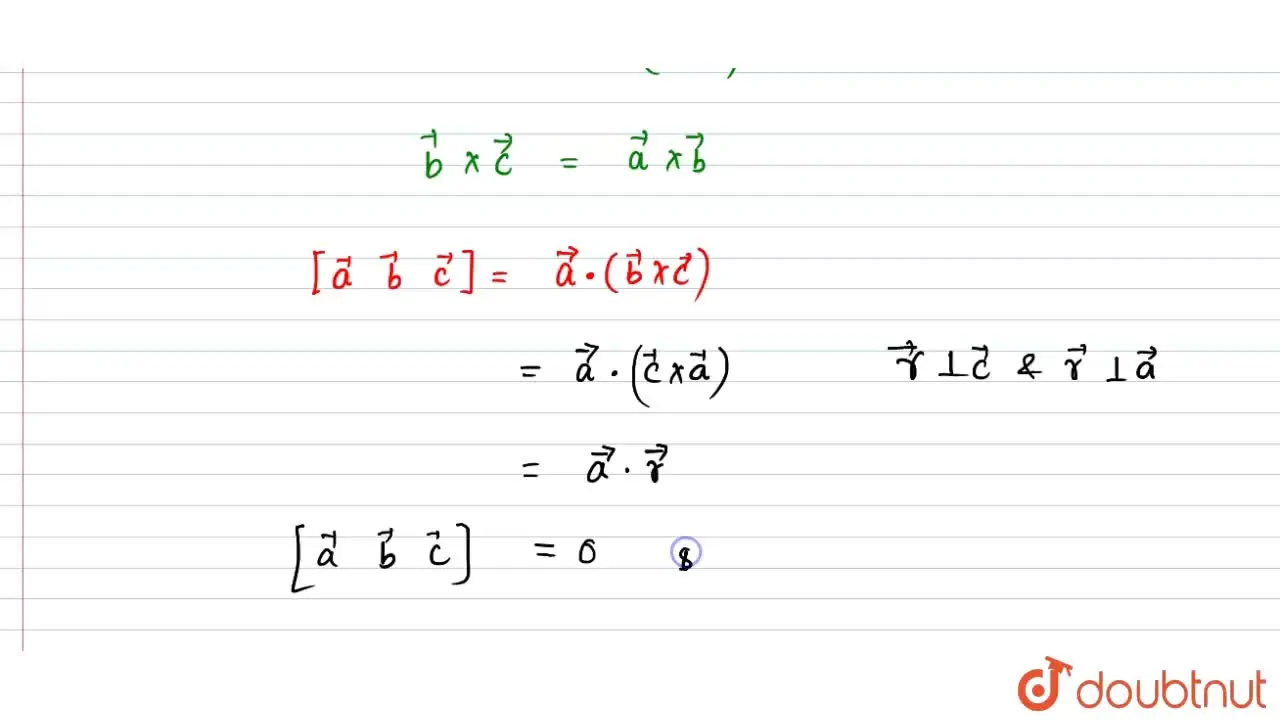If →a,→b,→c are three vectors such that →a+→b+→c=0, then prove that :
→a×→b=→b×→c=→c×→a and hence, show that [→a→b→c]=0.
Step by step video & image solution for If vec(a), vec(b), vec(c ) are three vectors such that vec(a)+vec(b)+vec(c )=0, then prove that : vec(a)xx vec(b)=vec(b)xx vec(c )=vec(c )xx vec(a) and hence, show that [vec(a)vec(b)vec(c )]=0. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - MODERN PUBLICATIONCHAPTER - VECTOR ALGEBRA EXERCISE - Objective Type Questions (A. Multiple Choice Questions)40videos
VECTOR ALGEBRA
- BOOK - MODERN PUBLICATIONCHAPTER - VECTOR ALGEBRA EXERCISE - Objective Type Questions (B. Fill in the Blanks)17videos
VECTOR ALGEBRA
- BOOK - MODERN PUBLICATIONCHAPTER - VECTOR ALGEBRA EXERCISE - EXERCISE 10 (j) Long Answer Type Questions (I)12videos
VECTOR ALGEBRA
- BOOK - MODERN PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - CHAPTER TEST 1111videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
If →a,→b,→c are three vectors such that →a+→b+→c=→0 , then prove that →a×→b=→b×→c=→c×→a
View SolutionIf →a+→b+→c=0, prove that (→a×→b)=(→b×→c)=(→c×→a)
View SolutionIf →a,→b,→c are three non-coplanar unit vector such that [→a,→b,→c]=3 then [→a×→b,→b×→c,→c×→a] equals
View SolutionIf →a,→band→c be three vectors such that →a+→b+→c=0 and |→a|=3,∣∣→b∣∣=5,∣∣→C∣∣=7, find the angle between →a and →b.
View SolutionIf →a,→b,→c are three vectors such that →a×→b=→c,→b×→c=→a, prove that →a,→b,→c are mutually at right angles and ∣∣→b∣∣=1,|→c|=|→a|.
View SolutionIf [→a→b→c]=4 then [→a×→b→b×→c→c×→a]=
View SolutionIf →b and →c are two non-collinear vectors such that →a∣∣(→b×→c) , then (→a×→b).(→a×→c) is equal to
View SolutionIf →a,→b and →c are mutually perpendicular unit vectors and →a×→b=→c, show that →b=→c×→a and →a=→b×→c.
View SolutionIf →a, →b, →c are three vectors such that →a.→b=→a.→c then show that →a=0 or, →b=c or →a⊥(→b−→c).
View SolutionIf →a,→b, →c are three vectors such that ∣∣→b∣∣=|→c| then {(→a+→b)×(→a+→c)}×{(→b×→c)}.(→b+→c)=
View Solution