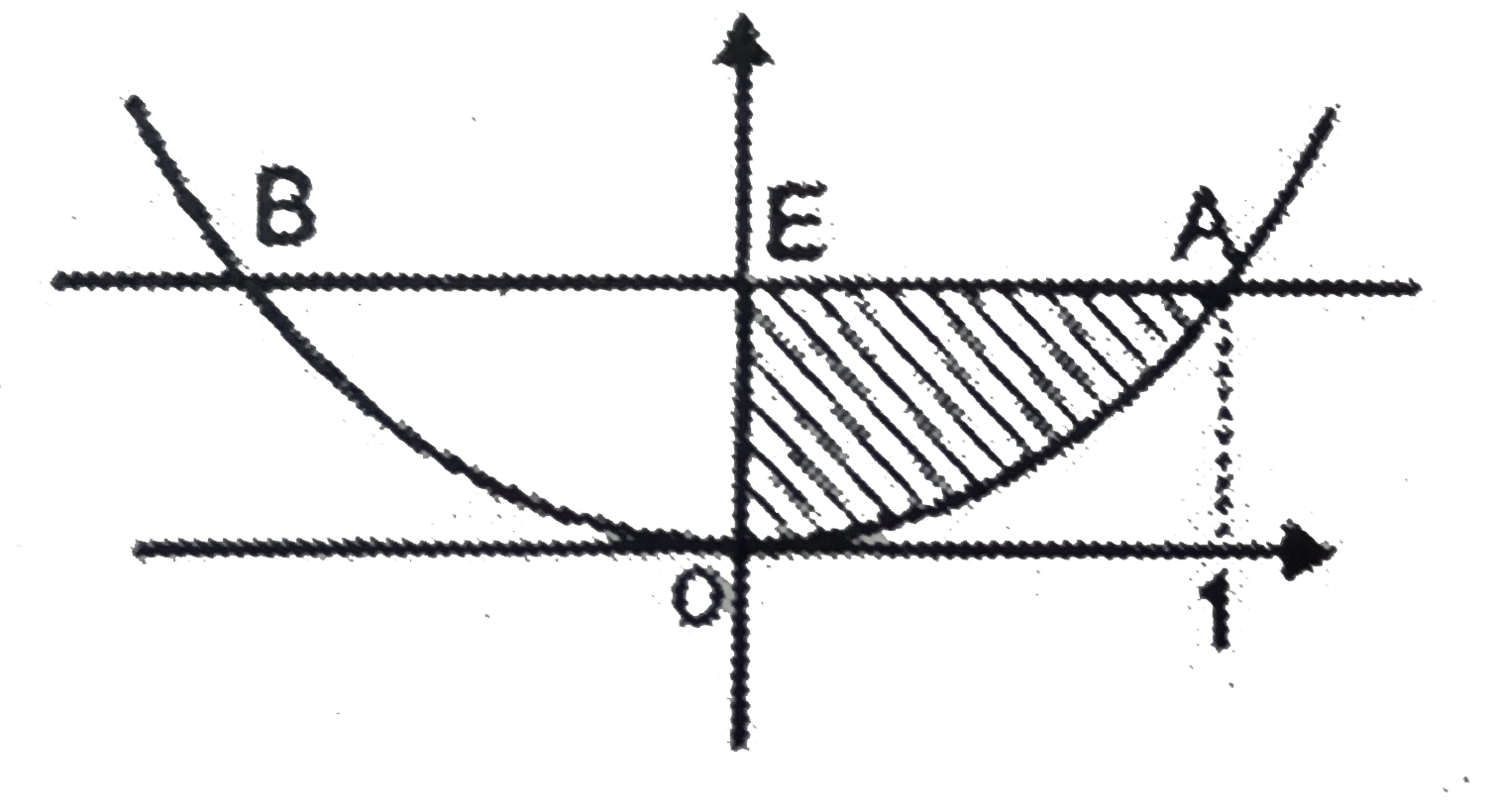
The area bounded by the parabola y2=8x, the x-axis and the latusrectum, is
Video Solution
Text Solution
The correct Answer is:323sq. units
|
Answer
Step by step video, text & image solution for The area bounded by the parabola y^(2)=8x, the x-axis and the latusrectum, is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATIONS OF THE INTEGRALS BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF THE INTEGRALS EXERCISE - QUESTIONS FROM NCERT BOOK (EXERCISE 8.1)
13 Videos
- APPLICATIONS OF THE INTEGRALS BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF THE INTEGRALS EXERCISE - QUESTIONS FROM NCERT BOOK (EXERCISE 8.2)
7 Videos
- APPLICATIONS OF THE INTEGRALS BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF THE INTEGRALS EXERCISE - OBJECTIVE TYPE QUESTIONS -TRUE/FALSE
5 Videos
- APPLICATIONS OF DERIVATIVESBOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - CHAPTER TEST (1)
12 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - MODERN PUBLICATIONCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - CHAPTER TEST
12 Videos
Similar Questions
Knowledge Check
Area bounded by the parabola ay2=x, the X-axis and the ordinate at x = a is
A2a23B2a3Ca22D3a22The area bounded by the parabola y=x2−7x+10 and X-axis
A9/2 sq unitsB1/6 sq unitsC5/6 sq unitsDNone of theseArea of the region bounded by the parabola ay=x2, the X-axis and the ordinates at x = a, x = 2a is
A3a27B3a7C7a3D7a23
The area bounded by the parabola y2=x along the X- axis & the lines x =0 , x= 2 is …… sq. units.
View SolutionFind the area of the region bounded by the parabola y2=4x, the x-axis, and the lines x = 1 and x = 4.
View SolutionFind the area bounded by the parabola x2=y, x-axis and the line y=1
View SolutionThe area bounded by the parabola y=4x−x2 and X-axis is
View SolutionThe area bounded by the parabola x2+8x+12y+4=0 and its latus rectum is 6k. Then the value of k is
View Solution
