If any two rows (or columns) of a determinant are identical, then the value of the determinant is zero.
The correct Answer is:1
To prove that if any two rows (or columns) of a determinant are identical, then the value of the determinant is zero, we can follow these steps:
Step 1: Define the Determinant
Let A be a determinant defined as follows:
A=∣∣
∣∣246246132∣∣
∣∣
Step 2: Modify One of the Rows
We can perform a row operation on the determinant. Specifically, we can subtract the first row from the second row:
R2→R2−R1
This gives us the new determinant:
A=∣∣
∣∣246000132∣∣
∣∣
Step 3: Expand the Determinant
Now, we can expand this determinant along the second row (which is now all zeros):
A=2⋅∣∣∣0032∣∣∣−0+0
Step 4: Calculate the Value
Since the second row is all zeros, the determinant evaluates to zero:
A=2⋅0−0+0=0
Step 5: Conclusion
Thus, we have shown that if two rows of a determinant are identical, the value of the determinant is zero.
Let A be a determinant defined as follows:
∣∣246246132∣∣
∣∣
We can perform a row operation on the determinant. Specifically, we can subtract the first row from the second row:
∣∣246000132∣∣
∣∣
Now, we can expand this determinant along the second row (which is now all zeros):
Since the second row is all zeros, the determinant evaluates to zero:
Thus, we have shown that if two rows of a determinant are identical, the value of the determinant is zero.
Topper's Solved these Questions
- DETERMINANTSBook:MODERN PUBLICATIONChapter:DETERMINANTSExercise:Competition file
Explore 14 Videos
- DETERMINANTSBook:MODERN PUBLICATIONChapter:DETERMINANTSExercise:Chapter test 4
Explore 12 Videos
- DETERMINANTSBook:MODERN PUBLICATIONChapter:DETERMINANTSExercise:Revision Exercise
Explore 32 Videos
- CONTINUITY AND DIFFERENTIABILITYBook:MODERN PUBLICATIONChapter:CONTINUITY AND DIFFERENTIABILITYExercise:CHAPTER TEST
Explore 12 Videos
- DIFFERENTIAL EQUATIONSBook:MODERN PUBLICATIONChapter:DIFFERENTIAL EQUATIONSExercise:CHAPTER TEST (9)
Explore 12 Videos
Similar Questions
Knowledge Check
If any two adjacent rows or columns of a determinant are intercharged in position, the value of the determinant :
ABecomes zeroBRemains the sameCChanges its signDIs doubledIf any two adjacent rows or columns of a determinant are interchanged in position, the value of the determinant
AA. Becomes zeroBB. Remains the sameCC. Changes its signDD. Is doubledIf each element in a row of a determinant is multiplied by the same factor r, then the value of the determinant
AA. Is multiplied by r3BB. Is increased by 3rCC. Remains unchangedDD. Is multiplied by r
If two rows (or column) are identical or Proportional the value of the determinant is
View SolutionIf any two rows(columns) of a square matrix A=[aij] of order (n≥2) are identical, then its determinant is 0.
View SolutionIn figure, determine the value of y.
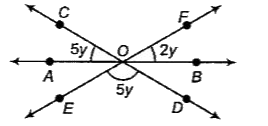
View SolutionIn figure, determine the value of y.

View SolutionThe element in the ith row and the jth column of a determinant of third order is equal to 2(i+j). What is the value of the determinant?
View Solution

