Two cells of internal resistance r1andr2 and of same emf are connected in series across a resistor of resistance R. If the terminal potential difference across the call of internal resistance r1 is zero , then the value of R is Solution in Kannada
R=2(r1+r2)
R=r2−r1
R=r1−r2
R=2(r1−r2)
The correct Answer is:C
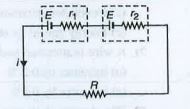
Let the emf of each cell be ε .
The cells are connected in series across R as shown in figure .
Since the cells are in series , so their equivalent emf is

εep=ε+ε=2ε
and their equivalent internal resistance is
req=r1+r2
The current in the circuit is
I=εeqreq+R=2εr1+r2+R ...(i)
The terminal potential difference across the cell of internal resistance r1 is
V1=ε=Ir1
But as per question V1=0
∴0=ε−Ir1 or I=εr1 ...(ii)
Equating (i) and (ii) , we get
2εr1+r2+R=εr1 or 2r1=r1+r2+R
or, R=2r!−r1−r2=r1−r2
Topper's Solved these Questions
Similar Questions
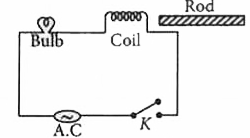
In the A. C. circuit shown, keeping 'K' pressed, if an iron rod is inserted into the coil, the bulb in the circuit
View SolutionWhich one of the following nuclei has shorter mean life?
View SolutionTwo sources of equal emf are connected to an external resistance R. The internal resistance of the two sources are R1andR2(R1>R1). if the potential difference across the source having internal resistance R2 is zero, then
View SolutionTwo sources of current of equal emf are connected in series and having different internal resistance r1 and r2(r2>r1). Find the external resistance R at which the potential difference across the terminals of one of the sources becomes equal to zero.
View SolutionTwo cells each emf e but of internal resistance r1 and r2 are connected in series through and external resistance R. IF the potential difference across the first cell is zero while current flows the value of R in terms of r1 and r2 is
View SolutionTwo cells each of emf e but internal resistances r_1 and r_2 are connected in series through an external resistance R. IF the potential difference across the first cell is zero while current flows,the relation of R in terms of r_1 and r_2 is
View SolutionTwo cells of same emf ε but internal resistances r1 and r2 are connected in series to an external resistor R. What should be the value of R so that the potential difference across the terminals of the first cell becomes zero.

View SolutionTwo cells of same emf ε but of different internal resistances r1 and r2 are connected in series with an external resistance R. The potential drop across the first cell is found to be zero. The external resistance R is
View SolutionA cell of emf 1.1 V and internal resistance r is connected across as external resister of resistance 10r. Find the potential difference across the external resistor.
View SolutionInternal resistance of battery of emf 2E is R_1 and battery of emf E is R_2 . If the potential difference across the cell of emf 2E is zero, then value of R is
View SolutionTwo sources of equal emf are connected in series and having different internal resistance r1 and r2(r2>r1). Find the external resistance R at which the potential difference across the terminals of one of the sources becomes equal to zero.
View SolutionIf the potential difference across the internal resistance r1 is equal to the emf E of the battery, then
View SolutionTwo cells each of emf e but internal resistance r1 and r2 are connected in series through an external resistance R. IF the potential difference across the first cell is szero while current flow, the relation of R in terms of r1 and r2
View SolutionA cell of emf E is connected across a conductor of resistance R. If the potential difference across the terminals of the conductor is found to be V, then the internal resistance of the cell is
View Solutionदो सेल समान वि.वा.ब. तथा r1,r2,(r1>r2) आन्तरिक प्रतिरोध के हैं, जो बाह्य प्रतिरोध R के साथ श्रेणी क्रम में जुड़े है। बंद परिपथ में पहले सेल का विभवांतर शून्य है तो R का मान :
View Solution

