In the reaction, R−Xalcoholic KCN−−−−−−−→Adilute HCl−−−−−→B the product B is Solution in Kannada
alkyl chloride
aldehyde
carboxylic acid
ketone
The correct Answer is:C
R−Xalkyl halidealcoholic KCN−−−−−−−→R−CNalkyl cyanidedil.HCl−−−−→R−COOHcarboxylic acid
Topper's Solved these Questions
Similar Questions
15 moles of H2 and 5.2 moles of I2 are mixed and allowed to attain equilibrium at 500∘C. At equilibrium, the concentration of HI is found to be 10 moles. The equilibrium constant for the formation of HI is
View SolutionThe number of unidentate ligands in the comples ion is called
View SolutionThe end product of the reaction,
Ethyl amine HNO2−−−→(A)PCl5−−→(B)KCN−−→(C) (C) is,
View SolutionIn the reaction, R-X overset("Alcoholic KCN") to A overset("Dil. HCl")toB The product B is
View SolutionThe product D of the reaction CH_(3)Cl overset( KCN) ( rarr) ( A) overset( H_(2) O) ( rarr) (B) overset( NH_(3))(rarr) ( C ) overset( Delta)( rarr) ( D ) is
View SolutionA and B in the following reaction are
R - C - R' HCN/KCN−−−−−−→B−−→
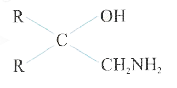
View Solutionअभिक्रिया का अंतिम उत्पाद Z होगा -
एथिलऐमीन HNO2−−−→XPCl5−−→YKCN−−→Z. Z है -
View SolutionIn the following sequence of reactions CH_3Br overset(KCN)(rarr)A overset(H_2O^(+))(rarr)B overset(LiA//H_4)(rarr)
View Solutionअभिक्रिया में, R−Xएल्कोहॉलिकKCN−−−−−−−−−→A तनुHCl−−−−→B उत्पाद B है
View SolutionIdentify (Z) in the following reaction series, C_2H_5I overset(Alcoholic KOH)rarr (X) overset(Br_2)rarr(Y)overset(KCN)rarr(Z)
View SolutionIdentified A and B in the following reactions. C_6H_5CH_2Br overset(alc)underset (KCN)rarr A overset(Na//ethanol)rarr B .
View SolutionIdentify (Z) in the following reaction series,
C2H5IAlcoholicKOH−−−−−−−−→(X)Br2−−→(Y)KCN−−→(Z)
View SolutionIdentify A and B : CH3CH2BrKCN−−→ALiAlH4−−−→B
View SolutionGive the structures of A and B in the following reactions: C2H5BrKCN−−→ALiAIH4−−−−→B
View SolutionThe end product of the reaction,
Ethyl amine HNO2−−−→(A)PCl5−−→(B)KCN−−→(C) (C) is,
View SolutionThe product D of the reaction CH3ClKCN−−→(A)H2O−−→(B)NH3−−→(C)Δ−−→(D) is
View Solution

