LCR श्रेणी अनुनादी परिपथ में प्रत्यावर्ती धारा का आवृत्ति के साथ परिवर्तन दर्शने वाला वक्र खीचिए तथा बैण्ड चौड़ाई के लिए च्यंजक प्राप्त कीजिए।

Video Solution

Text Solution

Verified by Experts

प्रत्यावर्ती धारा का आवृत्ति के साथ वक्र

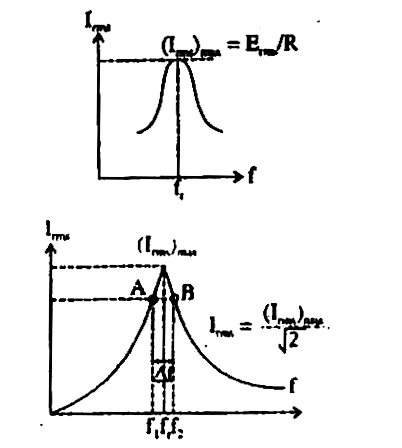
श्रेणी R-L-C परिपथ में $I_{r m s}$ तथा f के मध्य खींचे गये ग्राफ (चित्र) में अनुनादी आयृत्ति के दौनों ओर दो आवृत्तियाँ $f_{1} व f_{2},$ इस प्रकार ज्ञात की जाती हैं कि इन आवृतियों पर धारा का वर्ग माध्य मूल मान अपने अधिकतम ${(I_{r m s})}_{max} का \frac{1}{\sqrt{2}}$ होता हो या शक्ति क्षय अपने अनुनादी मान का आधा होता है इन आवृद्तियोँ $(f_{1} & f_{2})$ को अर्द्धशक्ति आवृत्तियोँ (half -power frequencies) कहते हैं। इन आवृत्तियों के संगत वक्र के बिन्दु A तथा B अर्द्दशक्ति बिन्दु कहलाते हैं।
बैण्ड चौड़ाई $(Band width - β = △ f)$ - अर्द्धशक्ति बिन्दुओं A व B संगत आवृत्तियों के इस अन्तर $(△ f = f_{2}, - f_{1})$ को श्रेणी अनुनादी परिपथ की ब्रैड कहा जाता है।
अतः बैण्ड चौड़ाई $β या △ f = f_{2} - f_{1}$
अनुनादी आवृत्ति $(f_{r})$ तथा बैण्ड चौड़ाई $(β)$ के अनुपात को परिपथ का विशेषता गुणांक कहते हैं।
विशेषता गुणांक $Q = \frac{f_{r}}{f_{2} - f_{1}}$ इसका मात्रक इकाई राहित होता है। अत: अर्द्ध शक्ति आवृतियी $F_{1} व F_{2}$ के लिए
$I_{r m s} = \frac{(I_{r m s}) max}{\sqrt{2}} ... ... . . (1)$
या $\frac{E_{r m s}}{\sqrt{R^{2} + (ω L - \frac{1}{{(ω C)}^{2}}) = \frac{E_{r m s}}{\sqrt{2} R}}}$
या $R^{2} + (ω L - \frac{1}{ω C} = 2 R^{2}$
या ${(ω L - \frac{1}{ω C})}^{2} = R^{2}$
या $ω L - \frac{1}{ω C} = \pm R ... ... ... . . (2)$
बिंन्दु A के लिए $ω_{1} L = \frac{1}{ω_{1} C} = - R ... ... (3)$
बिंन्दु B के लिए $ω_{2} L = \frac{1}{ω_{2} C} = - R ... ... . . (4)$
समीकरण (3) व (4) जो जोड़ने पर
$(ω_{2} + ω_{2}) L - (\frac{ω_{1} + ω_{2}}{ω_{1} ω_{2}} \frac{1}{C} = 0$
या $ω_{1} ω_{2} = \frac{1}{L C} = ω_{r}^{2} ... ... ... . (5)$
समीकरण (5) से $ω_{1} - ω_{2} = \frac{1}{L C} रखने पर$
अंत: $(ω_{2} - ω_{1}) L + (ω_{2} - ω_{1}) L = 2 R$
$\Rightarrow (ω_{2} - ω_{1}) \times 2 L = 2 R$
$\Rightarrow (ω_{2} - ω_{1}) = \frac{R}{L} = बेण्ड चौड़ाई$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

TRIPUTI PUBLICATION-वैघुत चुम्बकीय प्रेरण तथा प्रत्यावर्ती धारा-निबन्धात्मक प्रश्न

Home
Ask Doubt
Profile