Find the cube roots of the following using prime factorisation method
5832
19683
9261
405224
The correct Answer is:(a)18 (b)27 (c )21 (d)74
To find the cube roots of the given numbers using the prime factorization method, we will follow these steps:
Step 1: Prime Factorization
We will start by factorizing each number into its prime factors.
1. For the number 5, 8, 3, 2:
- 5 is a prime number.
- 8 = 2 × 2 × 2 = 23
- 3 is a prime number.
- 2 is a prime number.
- So, the prime factorization of 5, 8, 3, 2 is:
51×23×31
2. For the number 19683:
- 19683 can be factorized by dividing by 3:
- 19683 ÷ 3 = 6561
- 6561 ÷ 3 = 2187
- 2187 ÷ 3 = 729
- 729 ÷ 3 = 243
- 243 ÷ 3 = 81
- 81 ÷ 3 = 27
- 27 ÷ 3 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
- So, the prime factorization of 19683 is:
39
3. For the number 9261:
- 9261 can be factorized by dividing by 3:
- 9261 ÷ 3 = 3087
- 3087 ÷ 3 = 1029
- 1029 ÷ 3 = 343
- 343 = 73
- So, the prime factorization of 9261 is:
33×73
4. For the number 405224:
- 405224 can be factorized by dividing by 2:
- 405224 ÷ 2 = 202612
- 202612 ÷ 2 = 101306
- 101306 ÷ 2 = 50653 (not divisible by 2 anymore)
- Now, factor 50653 by dividing by 37:
- 50653 ÷ 37 = 1371
- 1371 ÷ 37 = 37
- So, the prime factorization of 405224 is:
23×373
Step 2: Grouping the Factors
Now we will group the prime factors in sets of three to find the cube roots.
1. For 5, 8, 3, 2:
- The factors are 51, 23, and 31.
- Grouping gives us:
√(3)51×23×31=2×√(3)5×3=2×√(3)15
2. For 19683:
- The factors are 39.
- Grouping gives us:
√(3)39=39/3=33=27
3. For 9261:
- The factors are 33 and 73.
- Grouping gives us:
√(3)33×73=33/3×73/3=3×7=21
4. For 405224:
- The factors are 23 and 373.
- Grouping gives us:
√(3)23×373=23/3×373/3=2×37=74
Final Answers
- The cube root of 5, 8, 3, 2 is 2√(3)15.
- The cube root of 19683 is 27.
- The cube root of 9261 is 21.
- The cube root of 405224 is 74.
We will start by factorizing each number into its prime factors.
- 5 is a prime number.
- 8 = 2 × 2 × 2 = 23
- 3 is a prime number.
- 2 is a prime number.
- So, the prime factorization of 5, 8, 3, 2 is:
51×23×31
- 19683 can be factorized by dividing by 3:
- 19683 ÷ 3 = 6561
- 6561 ÷ 3 = 2187
- 2187 ÷ 3 = 729
- 729 ÷ 3 = 243
- 243 ÷ 3 = 81
- 81 ÷ 3 = 27
- 27 ÷ 3 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
- So, the prime factorization of 19683 is:
39
- 9261 can be factorized by dividing by 3:
- 9261 ÷ 3 = 3087
- 3087 ÷ 3 = 1029
- 1029 ÷ 3 = 343
- 343 = 73
- So, the prime factorization of 9261 is:
33×73
- 405224 can be factorized by dividing by 2:
- 405224 ÷ 2 = 202612
- 202612 ÷ 2 = 101306
- 101306 ÷ 2 = 50653 (not divisible by 2 anymore)
- Now, factor 50653 by dividing by 37:
- 50653 ÷ 37 = 1371
- 1371 ÷ 37 = 37
- So, the prime factorization of 405224 is:
23×373
Now we will group the prime factors in sets of three to find the cube roots.
- The factors are 51, 23, and 31.
- Grouping gives us:
√(3)51×23×31=2×√(3)5×3=2×√(3)15
- The factors are 39.
- Grouping gives us:
√(3)39=39/3=33=27
- The factors are 33 and 73.
- Grouping gives us:
√(3)33×73=33/3×73/3=3×7=21
- The factors are 23 and 373.
- Grouping gives us:
√(3)23×373=23/3×373/3=2×37=74
- The cube root of 5, 8, 3, 2 is 2√(3)15.
- The cube root of 19683 is 27.
- The cube root of 9261 is 21.
- The cube root of 405224 is 74.
Topper's Solved these Questions
- SQUARES AND SQUARE ROOTS AND CUBES AND CUBE ROOTS Book:PEARSON IIT JEE FOUNDATIONChapter:SQUARES AND SQUARE ROOTS AND CUBES AND CUBE ROOTS Exercise:Easy Type Question
Explore 5 Videos
- SQUARES AND SQUARE ROOTS AND CUBES AND CUBE ROOTS Book:PEARSON IIT JEE FOUNDATIONChapter:SQUARES AND SQUARE ROOTS AND CUBES AND CUBE ROOTS Exercise:Level1
Explore 35 Videos
- SQUARES AND SQUARE ROOTS AND CUBES AND CUBE ROOTS Book:PEARSON IIT JEE FOUNDATIONChapter:SQUARES AND SQUARE ROOTS AND CUBES AND CUBE ROOTS Exercise:Very short Answer Type Question
Explore 30 Videos
- SIMPLE INTEREST AND COMPOUND INTEREST Book:PEARSON IIT JEE FOUNDATIONChapter:SIMPLE INTEREST AND COMPOUND INTEREST Exercise:CONCEPT APPLICATION Level 3
Explore 9 Videos
- STATISTICS Book:PEARSON IIT JEE FOUNDATIONChapter:STATISTICS Exercise:CONCEPT APPLICATION (LEVEL II)
Explore 29 Videos
Similar Questions
Knowledge Check
Find the cube roots of the following using prime factorisation method
A5832B19683C9261D405224Find the cubes of the following using alternative method
A52B24C46D72
Find the square root of the following by prime factorisation
View SolutionFind the HCF and LCM of the following by prime factorisation method :
(i) 12,18,24 (ii) 15,25,45
View SolutionFind the HCF and LCM of the following pairs using prime factorisation method:
(i) 140 and 154 (ii) 504 and 735
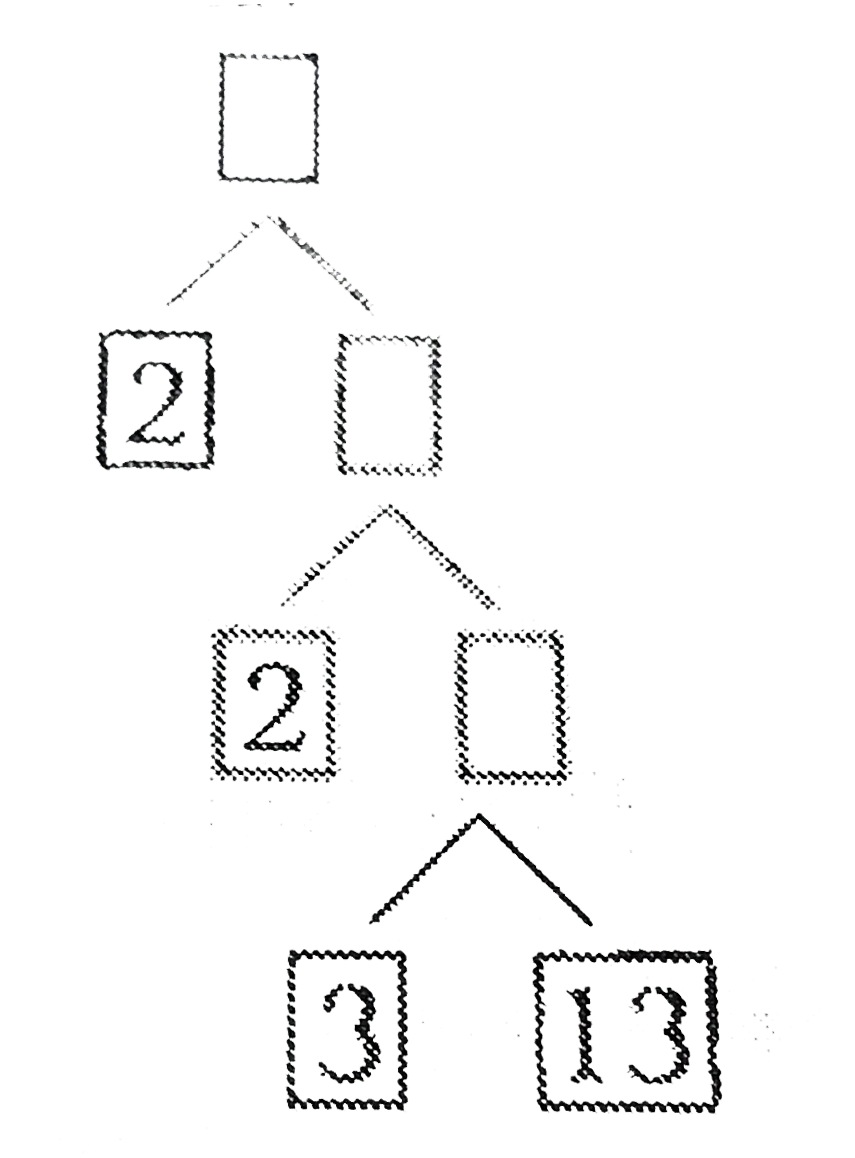
View SolutionFind the missing numbers in the following prime factorisation
View SolutionFind the cube root of each of the following numbers by prime factorisation method. 110592
View SolutionFind the cube root of each of the following numbers by prime factorisation method. 46656
View Solution
