A die is thrown 1000 times with the frequencies for the outcomes 1, 2, 3,4, 5 and 6 as given in the following table :Outcome123456Frequecny179150157149175190Find the probability of getting each outcome.
To find the probability of getting each outcome when a die is thrown 1000 times, we can follow these steps:
Step 1: Understand the Problem
We are given the frequencies of outcomes when a die is thrown 1000 times. We need to calculate the probability for each outcome (1, 2, 3, 4, 5, and 6).
Step 2: Gather the Data
From the problem, we have the following frequencies for each outcome:
- Outcome 1: 179
- Outcome 2: 150
- Outcome 3: 157
- Outcome 4: 149
- Outcome 5: 175
- Outcome 6: 190
Step 3: Calculate Total Frequency
The total number of times the die is thrown is given as 1000. This will be used as the denominator in our probability calculations.
Step 4: Calculate Probability for Each Outcome
The probability P of getting an outcome is calculated using the formula:
P(outcome)=Frequency of outcomeTotal frequency
Now, we will calculate the probability for each outcome:
1. Probability of Outcome 1:
P(1)=1791000=0.179
2. Probability of Outcome 2:
P(2)=1501000=0.150
3. Probability of Outcome 3:
P(3)=1571000=0.157
4. Probability of Outcome 4:
P(4)=1491000=0.149
5. Probability of Outcome 5:
P(5)=1751000=0.175
6. Probability of Outcome 6:
P(6)=1901000=0.190
Step 5: Summarize the Results
The probabilities for each outcome are:
- P(1)=0.179
- P(2)=0.150
- P(3)=0.157
- P(4)=0.149
- P(5)=0.175
- P(6)=0.190
We are given the frequencies of outcomes when a die is thrown 1000 times. We need to calculate the probability for each outcome (1, 2, 3, 4, 5, and 6).
From the problem, we have the following frequencies for each outcome:
- Outcome 1: 179
- Outcome 2: 150
- Outcome 3: 157
- Outcome 4: 149
- Outcome 5: 175
- Outcome 6: 190
The total number of times the die is thrown is given as 1000. This will be used as the denominator in our probability calculations.
The probability P of getting an outcome is calculated using the formula:
P(outcome)=Frequency of outcomeTotal frequency
P(1)=1791000=0.179
P(2)=1501000=0.150
P(3)=1571000=0.157
P(4)=1491000=0.149
P(5)=1751000=0.175
P(6)=1901000=0.190
The probabilities for each outcome are:
- P(1)=0.179
- P(2)=0.150
- P(3)=0.157
- P(4)=0.149
- P(5)=0.175
- P(6)=0.190
Similar Questions
A die is thrown 1000 times with the following frequencies for the outcomes 1, 2, 3, 4, 5 and 6 as given below: Outcome: 1 2 3 4 5 6 Frequency: 179 150 157 149 175 190 Find the probability of happening of each outcome.
View SolutionA dia is thrown 1000 times with the following frequencies for outcomes 1, 2, 3, 4, 5 and 6 as given below:
∣∣∣Outcome123456Frequency179150157149175190∣∣∣
Find the probability of happening of each outcome.
View Solution
Knowledge Check
A die is rolled 600 times and the occurrence of the outcomes 1, 2, 3, 4, 5 and 6 given below :
∣∣∣Outcome 1 2 3 4 5 6Frequency 200 30 120 100 50 100∣∣∣A13B12C14D15
A die is thrown 1000 times with the frequencies for the outcomes 1, 2, 3,4, 5 and 6 as given in the following table :Outcome123456Frequecny179150157149175190Find the probability of getting each outcome.
View SolutionA die is thrown 1000 times with the following frequencies for outcomes 1,2,3,4,5 and 6 as given below: Outcomes: 1 2 3 4 5 6 Frequency: 179 150 157 149 175 190 Find the probability of happening of each outcome.
View SolutionA dia is thrown 1000 times with the following frequencies for outcomes 1, 2, 3, 4, 5 and 6 as given below:
∣∣∣Outcome123456Frequency179150157149175190∣∣∣
Find the probability of happening of each outcome.
View SolutionA dice is rolled 100 times with the frequencies of the outcomes 1, 2, 3, 4, 5 and 6, which are given in the following table. Find the probaility of getting each outcome.
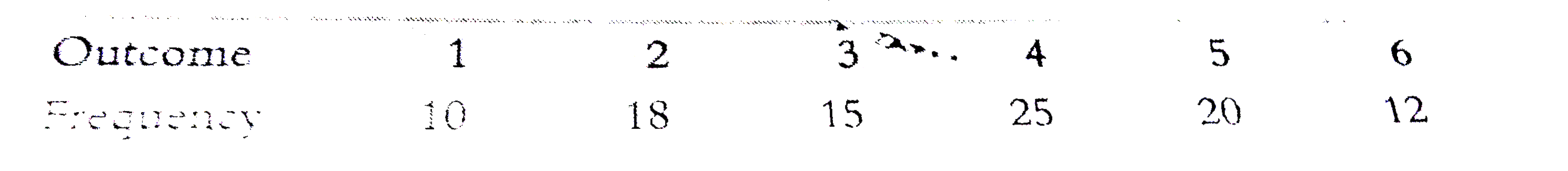
View SolutionA die is thrown 500 times with frequency for outcomes 1, 2, 3,4, 5, 6 as given below.Find the probability of getting an outcomes less than 4.
View SolutionA dice is rolled 600 times and the occurrence of the outcomes 1, 2, 3, 4, 5 and 6 are given below: Outcome 1 2 3 4 5 6 Frequency 200 30 120 100 50 100 The probability of getting a prime number is 13 (b) 23 (c) 4960 (d) 39125
View SolutionA dice is rolled 600 times and the occurrence of the outcomes 1, 2, 3, 4, 5 and 6 are given below in the table:
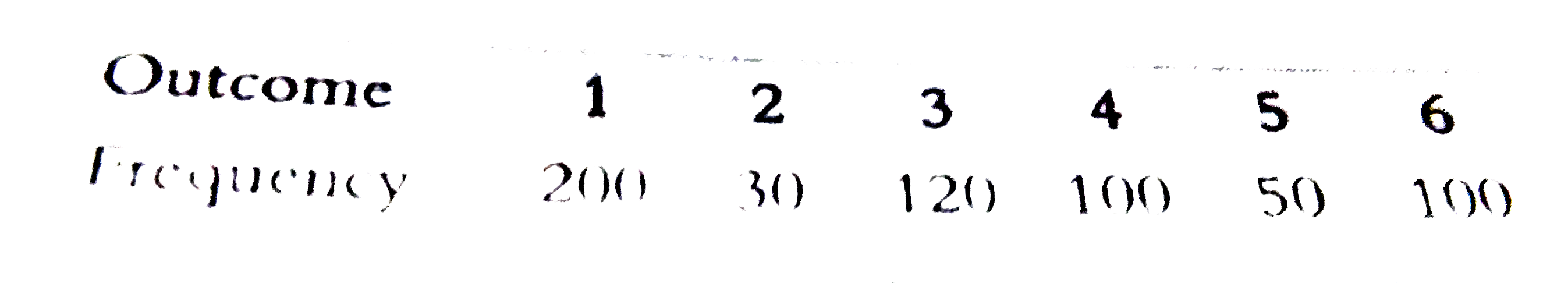
Find the probability of getting a prime number.
View Solution
