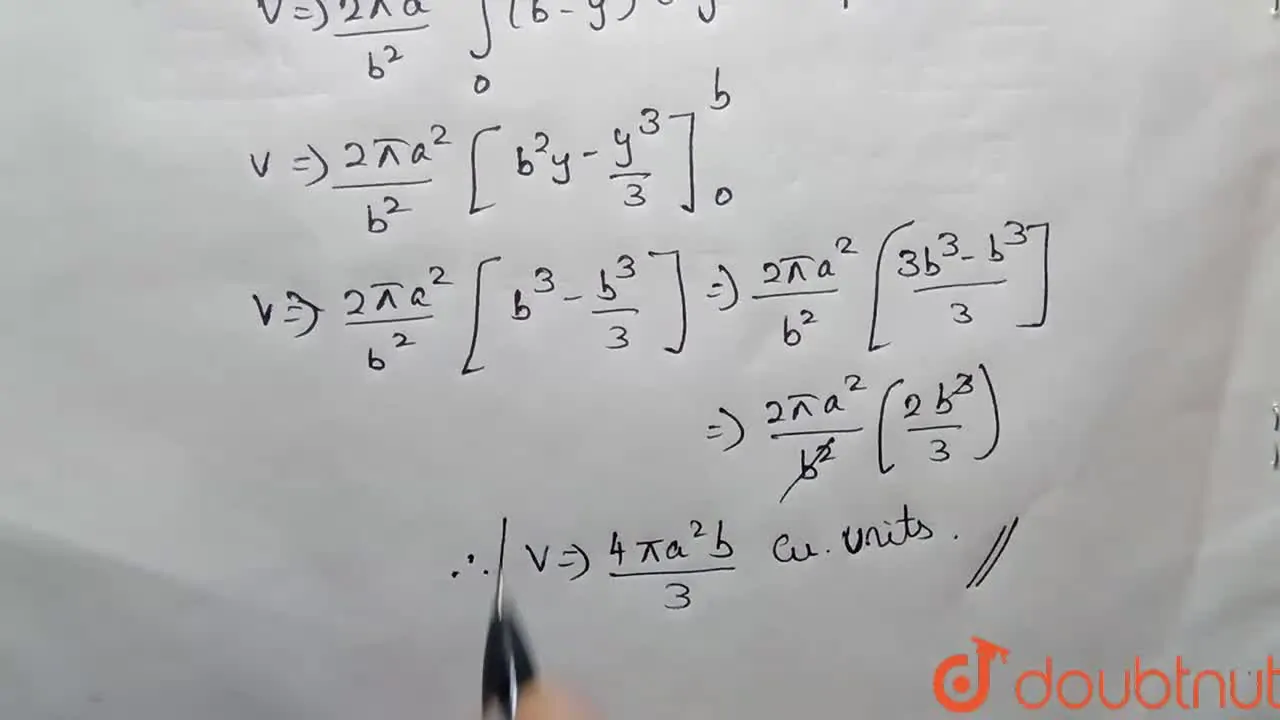The volume of the solid that results when the region enclosed by x2a2+y2b2=1 is revolved about the minor axis is :Solution in Tamil
The correct Answer is:4π3a2b cubic units
Step by step video, text & image solution for The volume of the solid that results when the region enclosed by (x^(2))/(a^(2)) +(y^(2))/(b^(2)) = 1 is revolved about the minor axis is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - FULL MARKSCHAPTER - APPLICATIONS OF INTEGRATIONEXERCISE - EXERCISE 9.1020videos
APPLICATIONS OF INTEGRATION
- BOOK - FULL MARKSCHAPTER - APPLICATIONS OF DIFFERENTIAL CALCULUS EXERCISE - ADDITIONAL QUESTIONS SOLVED56videos
APPLICATIONS OF DIFFERENTIAL CALCULUS
- BOOK - FULL MARKSCHAPTER - APPLICATIONS OF MATRICES AND DETERMINANTSEXERCISE - ADDITIONAL QUESTIONS SOLVED56videos
APPLICATIONS OF MATRICES AND DETERMINANTS
Similar Questions
The value of ∫230dx√4−9x2is
View SolutionA water tank has the shape of an invertd circular cone with base radius 2 metres and height 4 metres. If water is being pumped into the tank at the rate of 2m3/mm. Find the rate at which the water level is rising when the water is 3m deep
02:06View SolutionUsing elementary transformations find the inverse of the following matrix [4736]
02:30View SolutionThe volume of solid generated by revolving about the y-axis the figure bounded by the parabola y=x2andx=y2 is
02:46View SolutionFind,by integration, the volume of the solid generated by revolving about the x-axis, the region enclosed by y=2x2,y=0 and x=1.
04:12View SolutionFind, by integration , the volume of the solid generated by revolving about the x-axis, the region enclosed by y=e−2xy=0,x=0 and x=1
02:27View SolutionFind, by integration , the volume of the solid generated by revolving about the y-axis, the region enclosed by x2=1+y and y=3.
02:54View SolutionThe ratio of the volumes generated by revolving the ellipse x29+y24=1 about major and minor axes is
02:37View SolutionFind the volume of the solid generated when the region enclosed by y=√x,y=3andx=0 is revolved about y axis.
View SolutionFind the volume of solid that results when the region enclosed by the curve y=1+x2,x=0,x=2,y=0 is revolved about the x axis.
06:02View SolutionFind , by integration , the volume of the solid generated by revolving about y axis, the region bounded by the curve y=logx,y=0,x=0andy=2.
View SolutionThe volume of the solids obtained by revolving the area of the ellipse x2a2+y2b2=1 about major and minor axes in the ratio (a>b).
04:46View SolutionThe volume of solid obtained by revolving x29+y216=1 about the minor axis :
View SolutionThe volume of the solid formed by revolving the area of the circle x2+y2=9 about y axis is :
05:25View SolutionThe volume of the solid that results when the region enclosed by x2a2+y2b2=1 is revolved about the minor axis is :
View SolutionFind the volume of the solid formed by revolving the region bounded by the ellipsex2a2+y2b2=1,a>b about the major x-axis,
View Solution