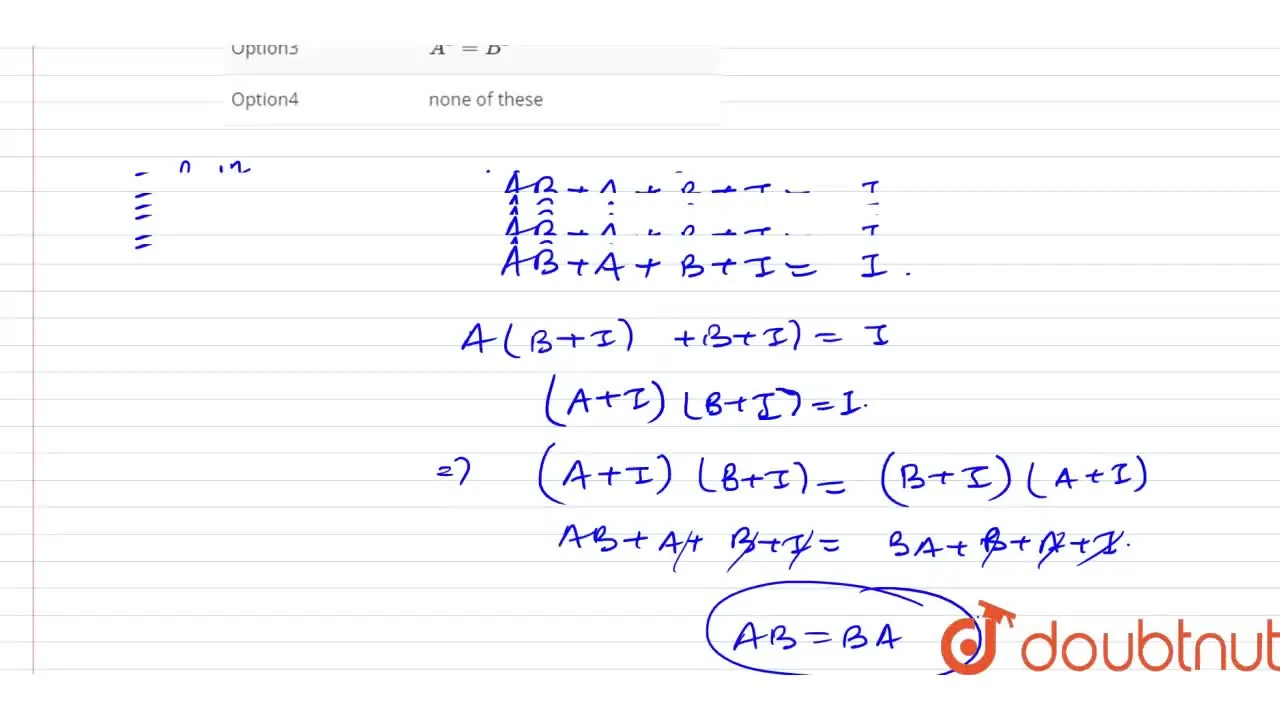
$A$ and $B$ be $3 \times 3$ matrices such that $A B + A = 0$ , then

A

${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

B

$| A | = | B |$

C

$A^{2} = B^{2}$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$(a)$ Given $A B + A + B = 0$
$\Rightarrow A B + A + B + I = I$
$\Rightarrow A (B + I) + (B + I) = ($
$\Rightarrow (A + I) (B + I) = I$
$\Rightarrow (A + I)$ and $(B + I)$ are inverse of each other
$\Rightarrow (A + I) (B + I) = (B + I) (A + I)$
$\Rightarrow A B = B A$
Thus $A$ and $B$ are commutative
$\Rightarrow {(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

|

Updated on:21/07/2023

Class 12 MATHS MATRICES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let $A$ and $B$ be two $3 \times 3$ matrices such that $A + B = 2 B'$ and $3 A + 2 B = I$ then
A $A - B = O$
B $A + B = I$
C $A - B = I$
D $A + 2 B = O$
Question 2 - Select One
If A and B are $3 \times 3$ matrices such that AB=A and BA=B, then
A $A^{2} = A and B^{2} = B$
B $A^{2} = A and B^{2} =! B$
C $A^{2} =! A and B^{2} = B$
D $A^{2} =! A and B^{2} =! B$
Question 3 - Select One
If A and B are $3 \times 3$ matrices such that $A^{2} - B^{2} = (A - B) (A + B)$ then
Aeither A or B is zero matrix
Beither A or B is unit matrix
CA=B
DAB=BA

CENGAGE-MATRICES-Single correct Answer

Home
Ask Doubt
Profile