For $a$ , $b$ , $c \in R - {0}$ , let $\frac{a + b}{1 - a b}$ , $b$ , $\frac{b + c}{1 - b c}$ are in $A . P .$ If $α$ , $β$ are the roots of the quadratic equation
$2 a c x^{2} + 2 a b c x + (a + c) = 0$ , then the value of $(1 + α) (1 + β)$ is

A

$0$

B

$1$

C

$- 1$

D

$2$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$(b)$ Given $\frac{a + B}{1 - a b}$ , $b$ , $\frac{b + c}{1 - b c}$ are in $A . P .$
$\Rightarrow b - \frac{a + b}{1 - a b} = \frac{b + c}{1 - b c} - b$
$\Rightarrow \frac{- a (b^{2} + 1)}{1 - a b} = \frac{c (b^{2} + 1)}{1 - b c}$
$\Rightarrow a + c = 2 a b c$
Now, given quadratic equation is
$2 a c x^{2} + 2 a b c x + 2 a b c = 0$
(Substituting $a + c = 2 a b c$ and then cancelling $2 a c$ )
$\Rightarrow x^{2} + b x + b = 0$

|

Updated on:21/07/2023

Class 12 MATHS PROGRESSION AND SERIES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $cot α and cot β$ are the roots of the equation $x^{2} + b x + c = 0$ with $b \neq 0$ then the value of $cot (α + β)$ is :
A $\frac{c - 1}{b}$
B $\frac{1 - c}{b}$
C $\frac{c}{c - 1}$
D $\frac{b}{1 - c}$
Question 2 - Select One
If $α$ and $β$ are the roots of the quadratic equation $x^{2} + b x - c = 0$ , then the equation whose roots are b and c, is
A $x^{2} + α x - β = 0$
B $x^{2} - [(α + β) + α β] x - α β (α - β) = 0$
C $x^{2} + [(α + β) + α β] x + α β (α + β) = 0$
D $x^{2} + [(α + β) + α β] x - α β (α + β) = 0$
Question 3 - Select One
Let $b = 6$ with a and c satisfying (1). If $α$ and $β$ are the roots of the quadeatic equation $a x^{2} + b x + c = 0, t h e n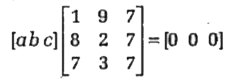$ is
A6
B7
C $\frac{6}{7}$
D $\infty$

CENGAGE-PROGRESSION AND SERIES-Single correct Answer

Home
Ask Doubt
Profile