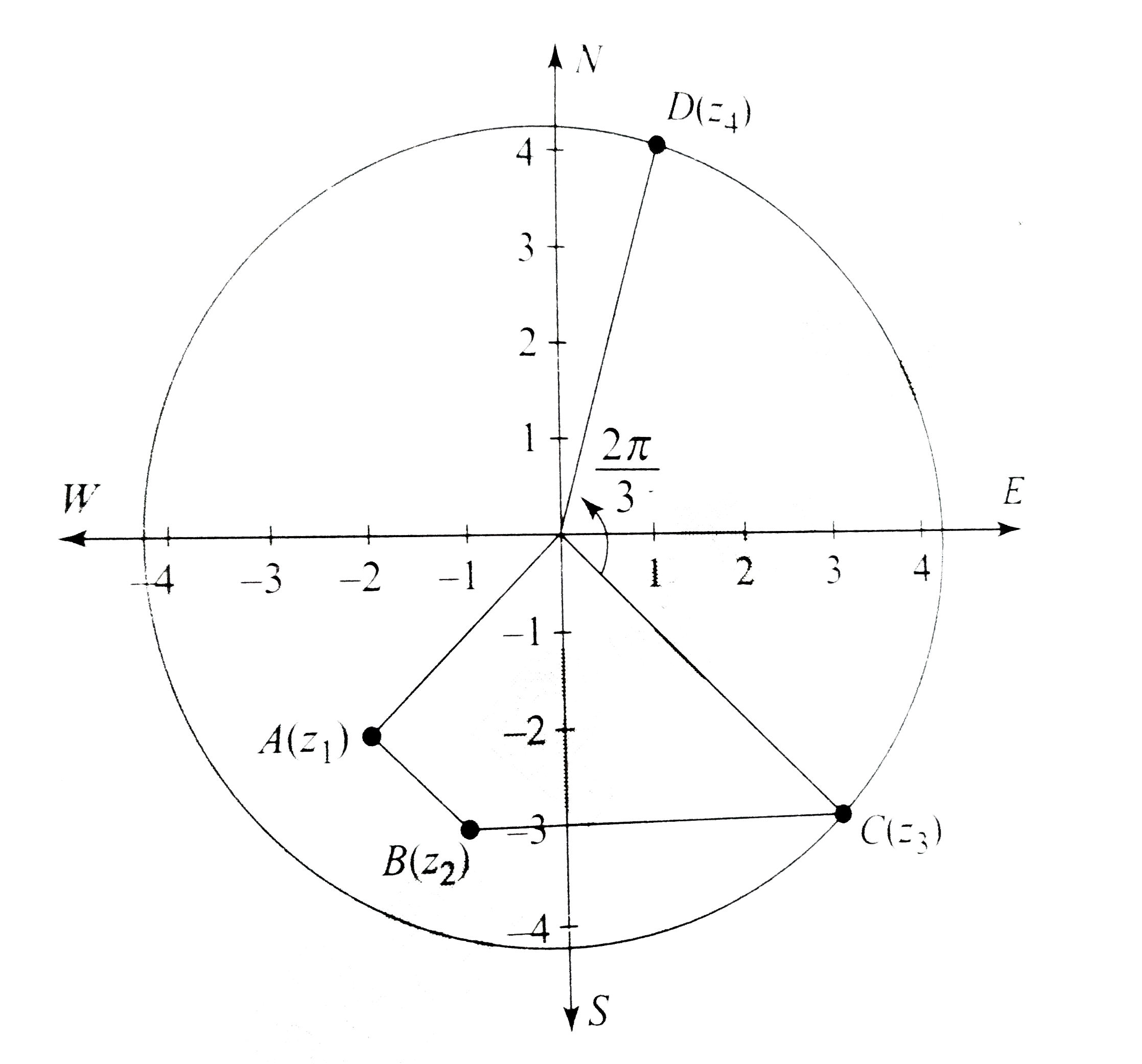
A person walks units away from origin in south west direction to reach , then walks units in south east direction to reach . From he travel is units horizontally towards east to reach . Then he travels along a circular path with centre at origin through an angle of in anti-clockwise direction to reach his destination .
Position of in argand plane is ( is an imaginary cube root of unity)
The correct Answer is:C
(rotation at )
(rotation at )
Topper's Solved these Questions
- COMPLEX NUMBERSBook:CENGAGEChapter:COMPLEX NUMBERSExercise:Examples
Explore 125 Videos
- COMPLEX NUMBERSBook:CENGAGEChapter:COMPLEX NUMBERSExercise:Exercise 3.1
Explore 4 Videos
- COMPLEX NUMBERSBook:CENGAGEChapter:COMPLEX NUMBERSExercise:Matching Column
Explore 1 Video
- CIRCLESBook:CENGAGEChapter:CIRCLESExercise:Question Bank
Explore 32 Videos
- CONIC SECTIONSBook:CENGAGEChapter:CONIC SECTIONSExercise:Solved Examples And Exercises
Explore 91 Videos
Similar Questions
A man walks a distance of 3 units from the origin towards north-east to reach position A. from there he walks a distance of 4 units towards North west to reach position P. Then position of P in argand plane is
View Solution'A' starts from origin and travels 1 unit distance along positive x-axis to reach P. From there he travels 2 unit parallel to y- axis to reach Q . Then the travels 3 unit distance parallel to y=x and away from origin to reach "R" .Then he rotates about O in anticlockwise direction so as to reach y-axis at S .If the co-ordinates of S are (0,S) then √2(S2−14) would be equal to
View Solution
Knowledge Check
A person walks 2√2 units away from origin in south west direction (S45∘W) to reach A, then walks √2 units in south east direction (S45∘E) to reach B. From B he travel is 4 units horizontally towards east to reach C. Then he travels along a circular path with centre at origin through an angle of 2π/3 in anti-clockwise direction to reach his destination D.
Let the complex number Z represents C in argand plane. then arg(Z)=A−π6Bπ4C−π4Dπ3A man walks a distance of 3 units from the origin towards the North-East (N450E) direction.From there, he walks a distance of 4 units towards the North-West (N450W) direction to reach a point P. Then, the position of P in the Argand plane is 3eiπ4+4i (b) (3−4i)eiπ4 (4+3i)eiπ4 (d) (3+4i)eiπ4
A3eiπ/4+4iB(3−4i)eiπ/4C(4+3i)eiπ/4D(3+4i)eiπ/4Nimisha started walking towards south to reach her school which is 5 km away. From there she turns 180∘ in clockwise and then 45∘ in anticlockwise direction. Which direction is she facing now from her school ?
ASouthBNorthCSouth-eastDNorth-west
Dipak walks from point P 15 m to the east to reach point Q. then he takes right turn and walks for 20 m to reach point R. now he takes a left turn and walks for 15m to reach point S. now he takes a left turn and walks for 10 m to reach point T. then he takes a right turn and walks for 5 m to reach point V. now ke takes a left turn and walks for 10m to reach point W.
Point R is in which direction with respect to point T?
View SolutionA particle starts from a point z0=1+i where i=√−1. lt moves horizontally away from origin by 2 units and then vertically away from origin by 3 units to reach a point z1, From z1 particle moves √5 units in the direction of 2ˆi+3ˆj and then it moves through à n angle of cosec−12 in anticlockwise direction of a circle with centre at origin to reach a point z2. The arg z1 is given by
View SolutionAkhil walks 2 km towards East and then turns left and walks 2 km. In which direction is he with respect to his initial position ?
View SolutionA particle P starts from the point z0=1+2i, where i=√−1. It moves first horizontally away from origin by 5 units and then vertically away from origin by 3 units in the direction of the vector ˆi+ˆj and then it moves through an angle π2 in anticlockwise direction on a circle with center at origin, to reach a point z2. The point z2 is given by
View SolutionA particle P starts from the point z0=1+2i, where i=√−1 . It moves first horizontally away from origin by 5 units and then vertically away from origin by 3 units to reach a point z1. From z1 the particle moves √2 units in the direction of the vector ˆi+ˆj and then it moves through an angle π2 in anticlockwise direction on a circle with centre at origin, to reach a point z2. The point z2 is given by 6+7i (b) −7+6i 7+6i (d) −6+7i
View Solution

