Formula of a growth which can be represented in linear curve as
L1=L0+rt
L0=L1+rt
W1=W0ert
W0=W1ert
The correct Answer is:A
To find the formula for growth that can be represented by a linear curve, we can follow these steps:
1. Understanding Growth Types:
- There are two main types of growth: Arithmetic and Geometric.
- Arithmetic growth is characterized by a constant addition of growth over time, while geometric growth involves exponential increase.
2. Identifying Linear Growth:
- Linear growth corresponds to arithmetic growth, where the increase is uniform over time.
- In arithmetic growth, the growth can be represented as a straight line on a graph, indicating that the growth rate remains constant.
3. Defining the Variables:
- Let:
- L0 = Initial length of the organ at time t=0
- R = Rate of growth (how much the length increases per unit of time)
- T = Time elapsed
4. Formulating the Equation:
- The length of the organ at time t can be expressed as:
L1=L0+R×T
- Here, L1 is the length of the organ at time t.
5. Understanding the Equation:
- This equation shows that the final length L1 is equal to the initial length L0 plus the product of the growth rate R and the time T.
- This linear relationship indicates that as time increases, the length increases at a constant rate, resulting in a linear curve when graphed.
6. Conclusion:
- Therefore, the formula of growth that can be represented by a linear curve is:
L1=L0+R×T
- There are two main types of growth: Arithmetic and Geometric.
- Arithmetic growth is characterized by a constant addition of growth over time, while geometric growth involves exponential increase.
- Linear growth corresponds to arithmetic growth, where the increase is uniform over time.
- In arithmetic growth, the growth can be represented as a straight line on a graph, indicating that the growth rate remains constant.
- Let:
- L0 = Initial length of the organ at time t=0
- R = Rate of growth (how much the length increases per unit of time)
- T = Time elapsed
- The length of the organ at time t can be expressed as:
L1=L0+R×T
- Here, L1 is the length of the organ at time t.
- This equation shows that the final length L1 is equal to the initial length L0 plus the product of the growth rate R and the time T.
- This linear relationship indicates that as time increases, the length increases at a constant rate, resulting in a linear curve when graphed.
- Therefore, the formula of growth that can be represented by a linear curve is:
L1=L0+R×T
Similar Questions
Growth curve is
View Solution(a) Name the two growth models that represent population growth and draw the respective growth curves they represent.
(b) State the basis for the difference in the shape of these curves.
(c) Which one of the curves represent the human population growth at present? Do you think such a curve is sustainable ? Give reason in support of your answer.
View Solution
Knowledge Check
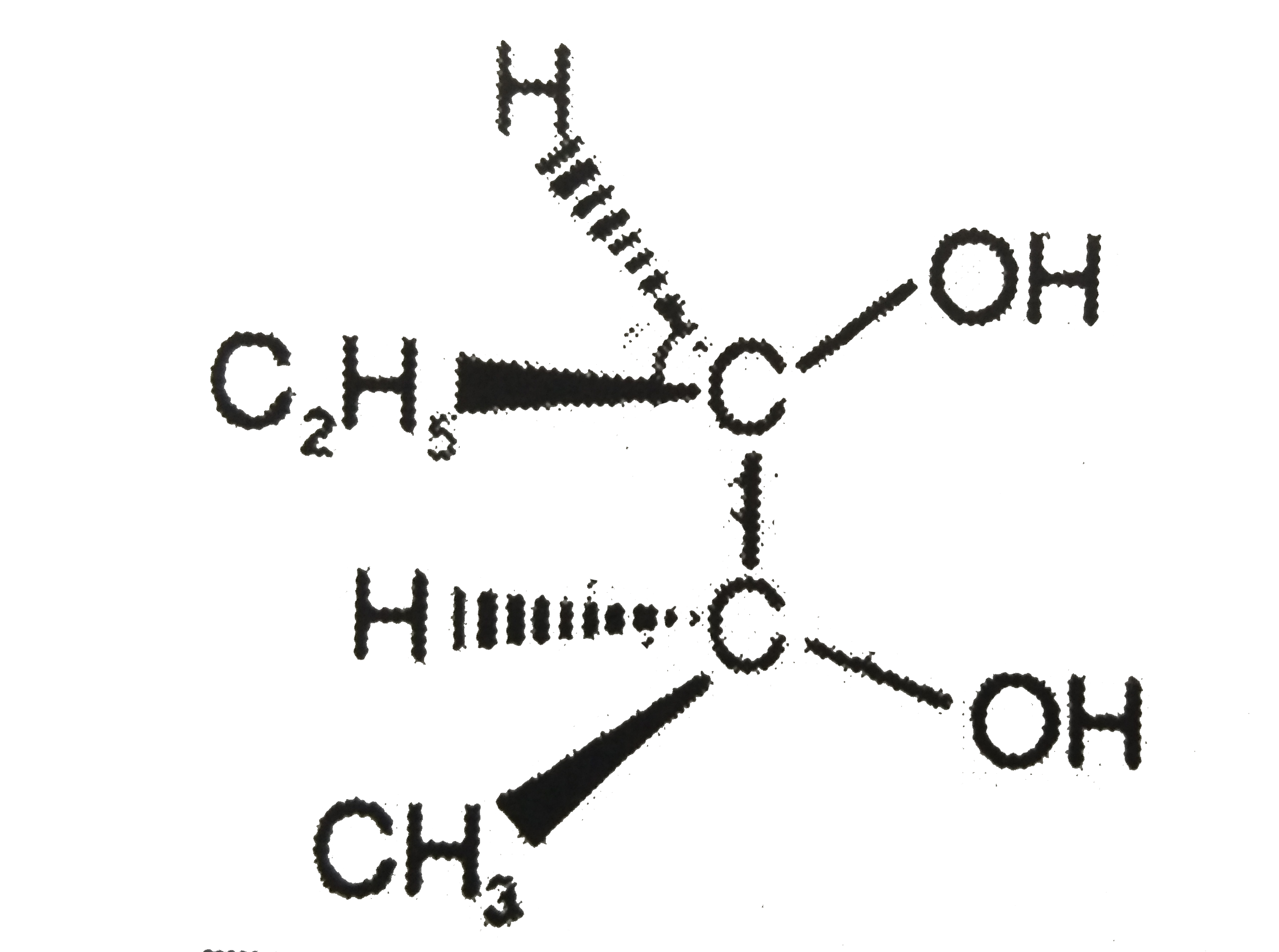
Fischer projection formula of this compound can be represented as :A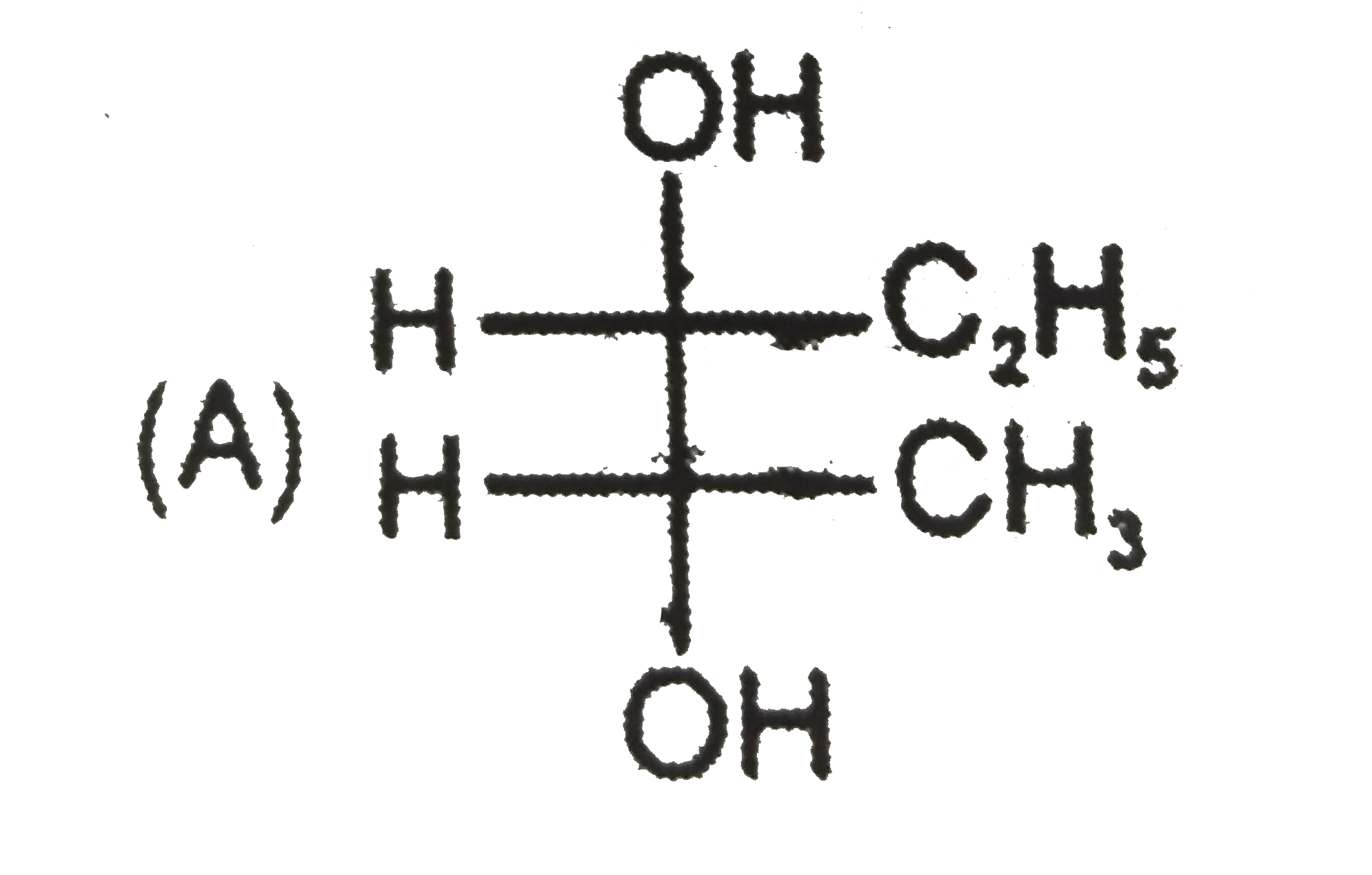 B
B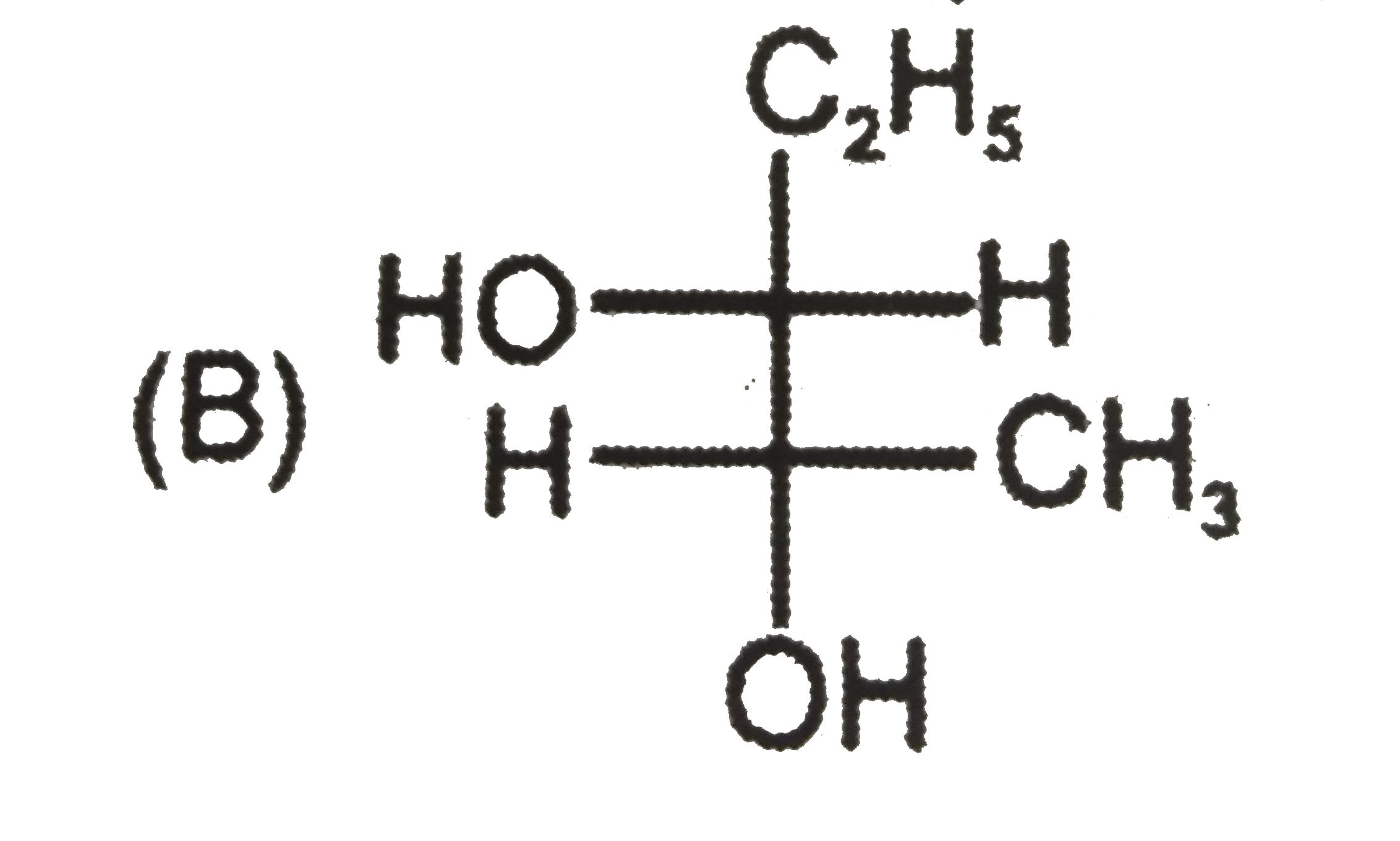 C
C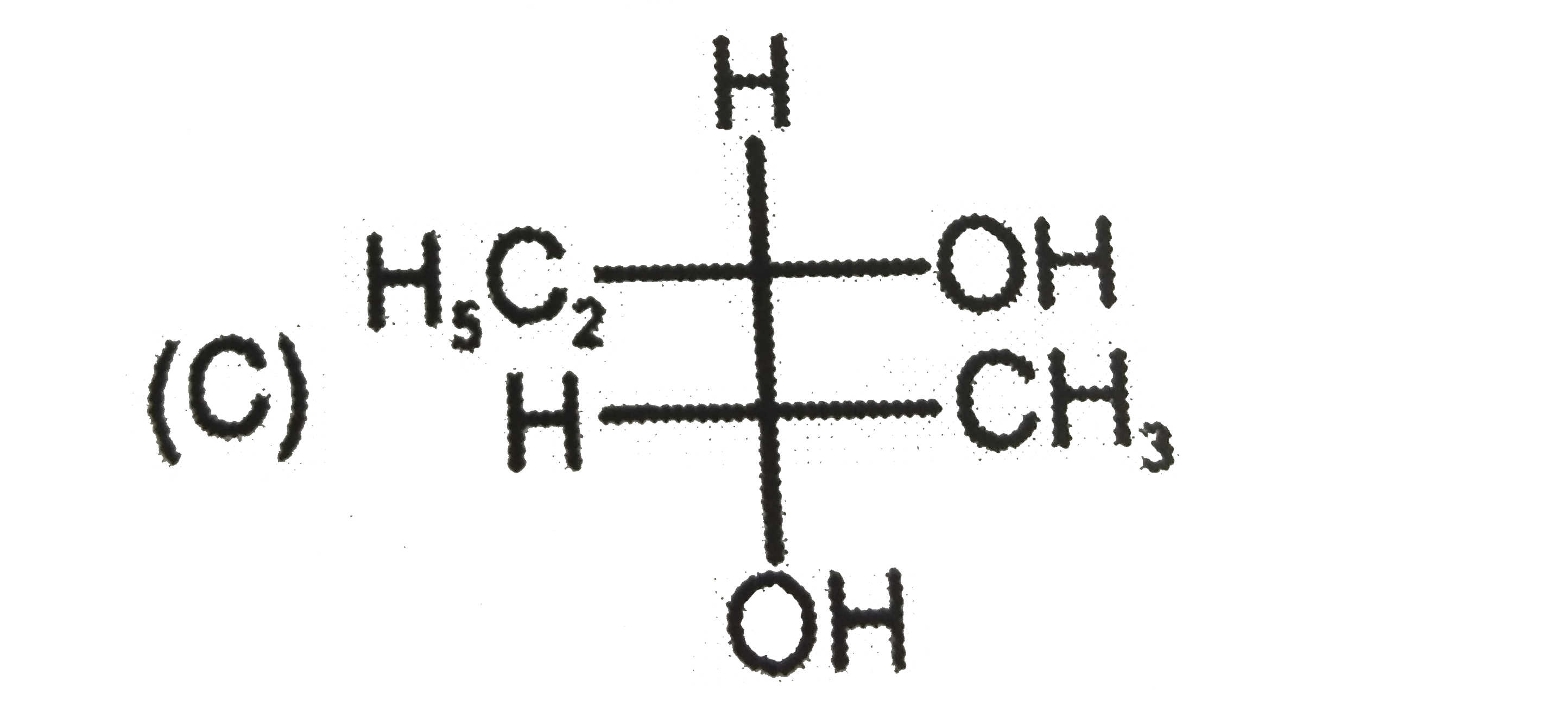 D
D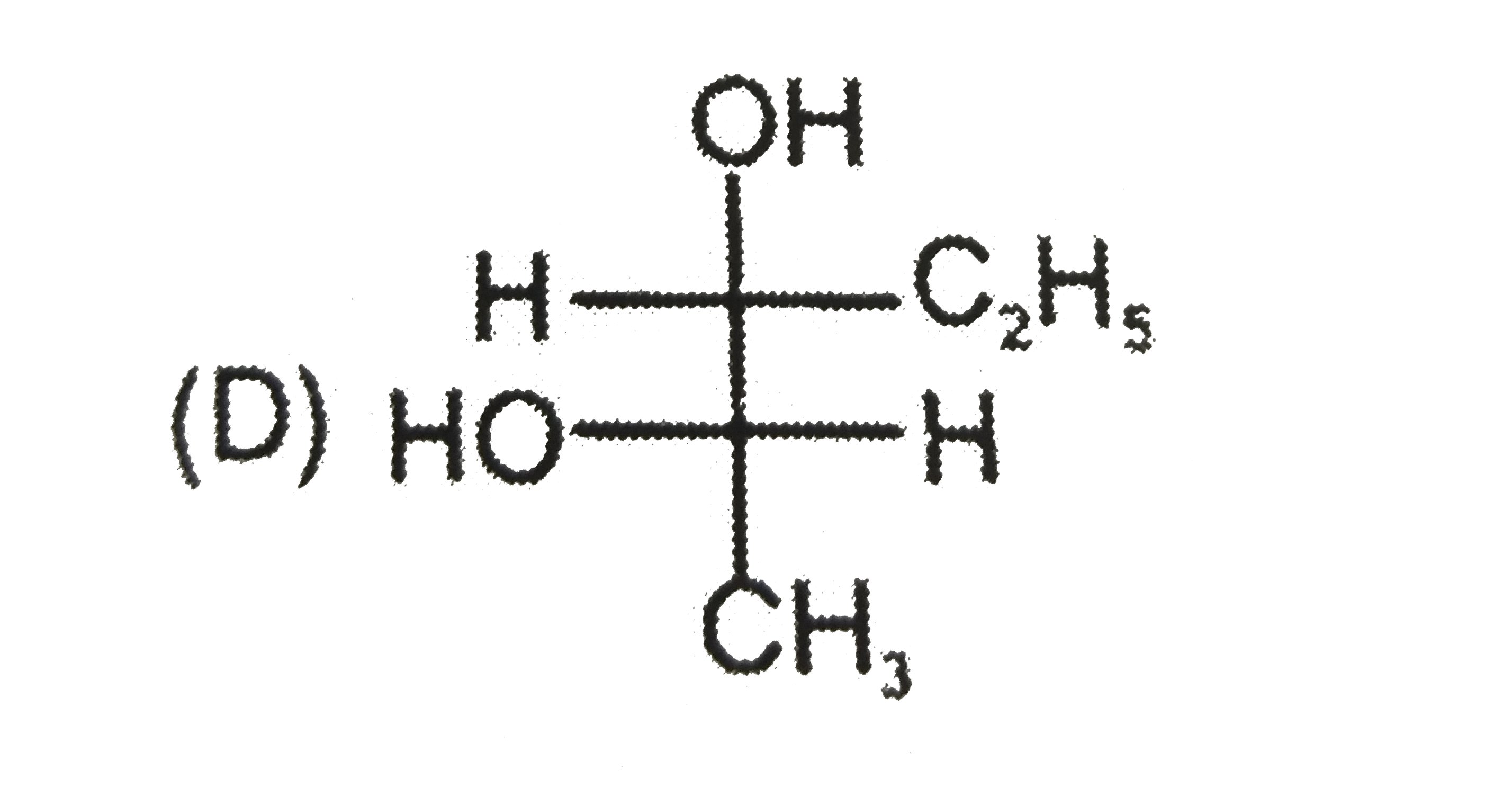
Which formula represent a salt?
ANaOHBKClCCH3OHDCH3−O∣∣C−CH3In tree, the growth ring represent -
APrimary xylemBSecondary xylemCSecondary phloemDCambium
Cl2 is used preparation of poisonous gases, one of them is mustard gas, which can be represented by the formula
View SolutionNormal shape of growth curve is,
View SolutionWhich of the following can represent a linear function for each x∈R ?
View SolutionGlyceryl oleate can be represented by the formula
View SolutionPerfectly elasticy demand is represented by a curve which is
View Solution
