Which of the following statement is not correct about order of a reaction ?
The order of a reaction can be a fractional number.
Order of a reaction is experimentally determined quantity.
the order of a reaction is always equal to the z sum of the stoichiometric coefficients o f reactants in the balanced chemical equation for a reaction,
The order of a reaction is the sum of the powers o f m olar concentration o f the reactants in the rate law expression
The correct Answer is:C
Step by step video, text & image solution for Which of the following statement is not correct about order of a reaction ? by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHEMICAL KINETICS BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -3
39 Videos
- CARBOXYLIC ACIDBOOK - NARAYNACHAPTER - CARBOXYLIC ACIDEXERCISE - All Questions
288 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - NARAYNACHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - ASSERTION & REASON TYPE QUESTIONS
10 Videos
Similar Questions
Knowledge Check
Which of the following statement is not correct about order of a reaction ?
AThe order of a reaction can be a fractional number.BOrder of a reaction is experimentally determined quantity.CThe order of a reaction is always equal to the sum of the stoichiometric coefficients of reactants in the balanced chemical equation for a reaction.DThe order of a reaction is the sum of the powers of molar concentration of the reactants in the rate law expression.Which of the following statement is not correct about order of a reaction ?
AThe order of a reaction is determined experimentally.BIt is the sum of the powers of concentration terms in the rate law expression.CIt does not necessarily depend on stoichiometric coefficients.DThe order of a reaction can not have a fractional value.Which of the following statement is incorrect about order of reaction
AOrder of reaction is determined experimentallyBIt is the sum of power of concentration terms in the rate law expressionCIt does not necessarily depend on stoichiometric coefficients.DOrder of the reaction can not have fractional value.
Which of the following statements about Be is not correct?
View SolutionWhich of the following statements are correct about this reaction ?
View SolutionWhich of the following statements is/are correct about the following reactions ?
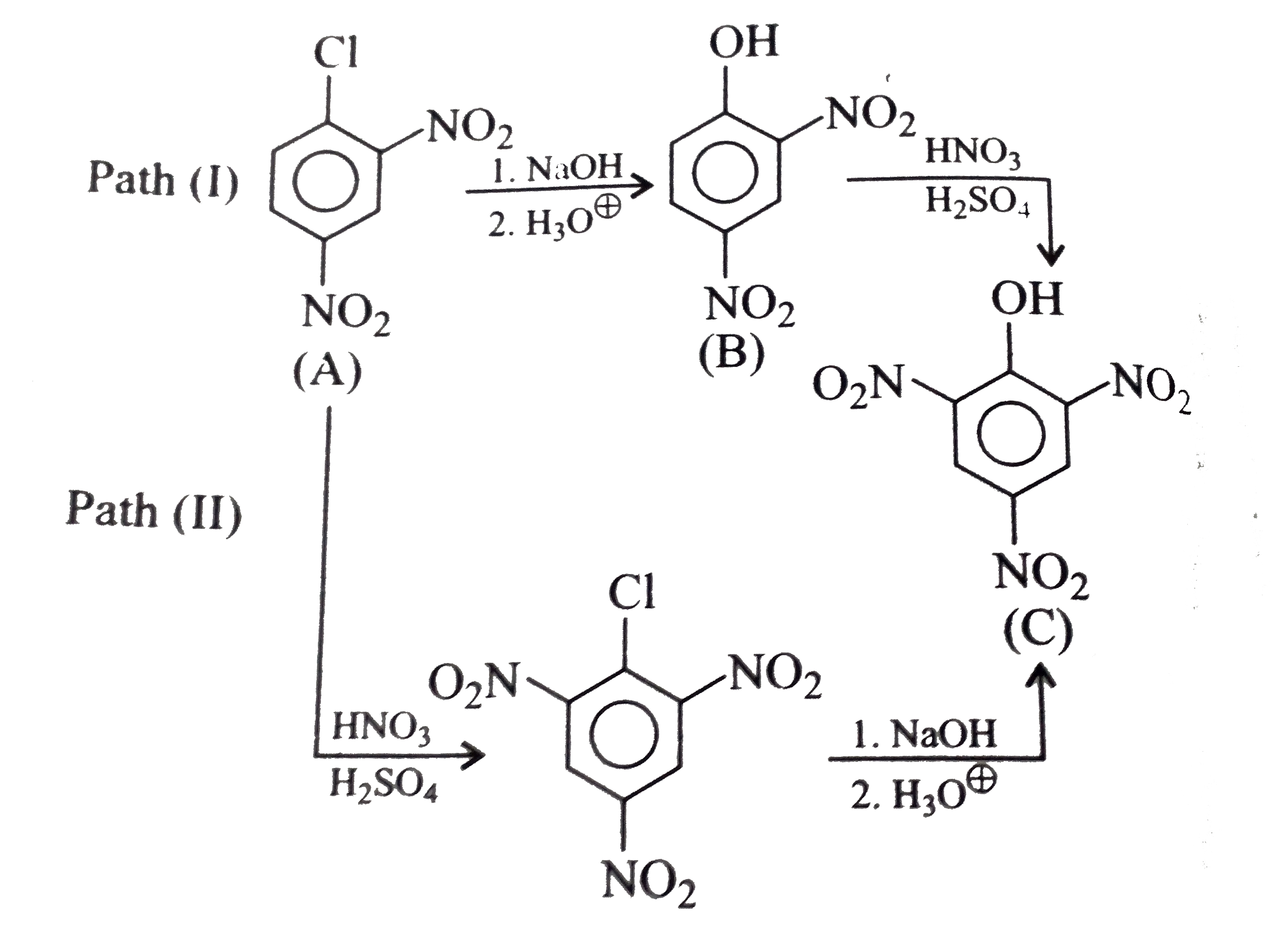
View SolutionWhich of the following statements is/are correct about the following reaction ?

View SolutionWhich of the following statements is/are correct about the following reaction ?
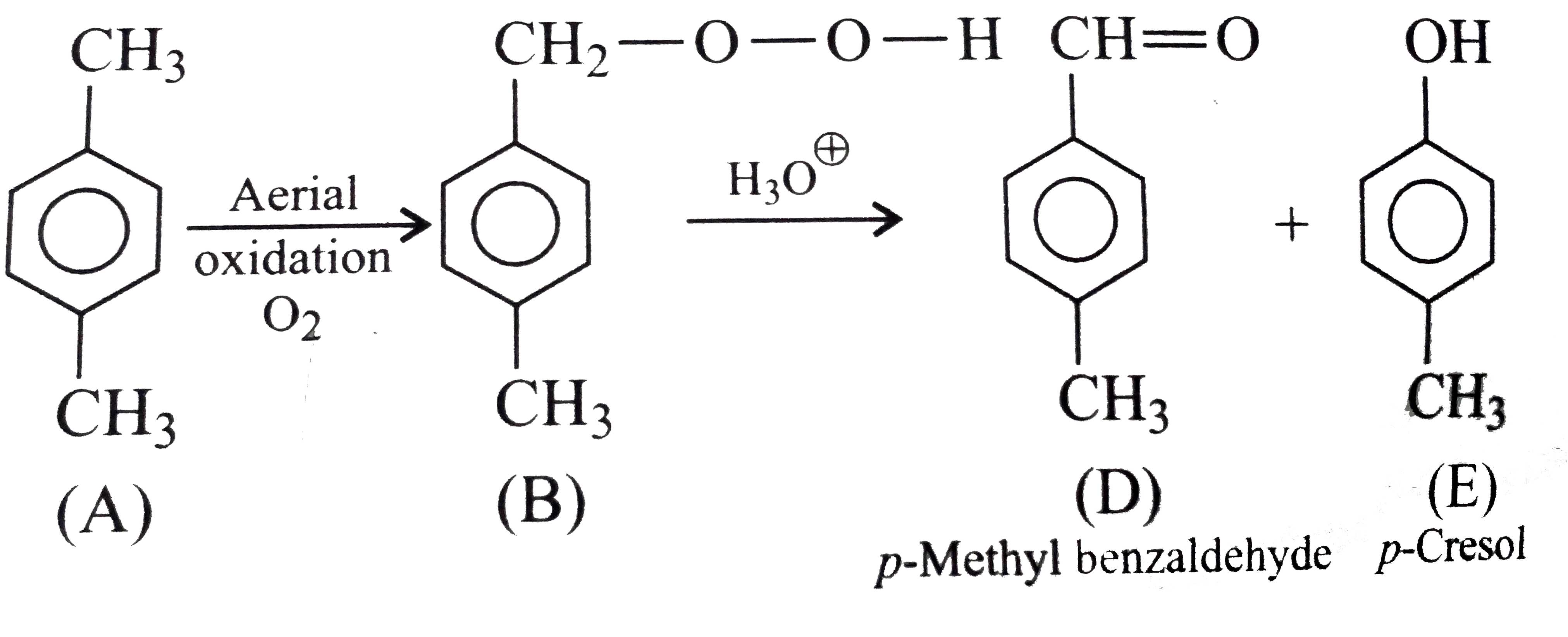
View Solution