The radioactive isotope 32P decays by first order kinetics and has a half-life of 14.3 days. How long does it take for 95.0% of a given sample of 32 p to decay?
21 days
42 days
62 days
80 days
The correct Answer is:C
To solve the problem of how long it takes for 95.0% of a given sample of the radioactive isotope 32P to decay, we will follow these steps:
Step 1: Determine the decay constant (k)
The decay constant k for a first-order reaction can be calculated using the half-life (t1/2) formula:
k=0.693t1/2
Given that the half-life t1/2=14.3 days, we can substitute this value into the equation:
k=0.69314.3≈0.0485 days−1
Step 2: Set up the first-order kinetics equation
For a first-order reaction, the relationship between the initial concentration (A0), the concentration at time t (A), and the amount that has decayed (x) can be expressed as:
t=2.303klog(A0A0−x)
Here, since we want to find the time taken for 95% decay, we can express x as:
x=0.95A0
Thus, A0−x=A0−0.95A0=0.05A0.
Step 3: Substitute values into the equation
Now we can substitute A0 and A0−x into the equation:
t=2.303klog(A00.05A0)
This simplifies to:
t=2.303klog(10.05)=2.303klog(20)
Step 4: Calculate the logarithm
Next, we calculate log(20):
log(20)=log(2×10)=log(2)+log(10)=0.3010+1=1.3010
Step 5: Substitute k and log(20) into the time equation
Now we can substitute k and log(20) into the equation for t:
t=2.3030.0485×1.3010
Step 6: Calculate t
Now we perform the calculation:
t=2.303×1.30100.0485≈2.9930.0485≈61.82 days
Step 7: Round the answer
Rounding 61.82 days gives us approximately 62 days.
Final Answer
Therefore, it takes approximately 62 days for 95.0% of the sample of 32P to decay.
---
The decay constant k for a first-order reaction can be calculated using the half-life (t1/2) formula:
k=0.693t1/2
Given that the half-life t1/2=14.3 days, we can substitute this value into the equation:
k=0.69314.3≈0.0485 days−1
For a first-order reaction, the relationship between the initial concentration (A0), the concentration at time t (A), and the amount that has decayed (x) can be expressed as:
t=2.303klog(A0A0−x)
Here, since we want to find the time taken for 95% decay, we can express x as:
x=0.95A0
Thus, A0−x=A0−0.95A0=0.05A0.
Now we can substitute A0 and A0−x into the equation:
t=2.303klog(A00.05A0)
This simplifies to:
t=2.303klog(10.05)=2.303klog(20)
Next, we calculate log(20):
log(20)=log(2×10)=log(2)+log(10)=0.3010+1=1.3010
Now we can substitute k and log(20) into the equation for t:
t=2.3030.0485×1.3010
Now we perform the calculation:
t=2.303×1.30100.0485≈2.9930.0485≈61.82 days
Rounding 61.82 days gives us approximately 62 days.
Therefore, it takes approximately 62 days for 95.0% of the sample of 32P to decay.
Topper's Solved these Questions
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:EXERCISE -2 (H.W) COLLISION THEORY
Explore 7 Videos
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:EXERCISE -3
Explore 39 Videos
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:EXERCISE -2 (H.W) (ORDER OF REACTION)
Explore 16 Videos
- CARBOXYLIC ACIDBook:NARAYNAChapter:CARBOXYLIC ACIDExercise:All Questions
Explore 288 Videos
- CHEMISTRY IN EVERYDAY LIFEBook:NARAYNAChapter:CHEMISTRY IN EVERYDAY LIFEExercise:ASSERTION & REASON TYPE QUESTIONS
Explore 10 Videos
Similar Questions
The reaction A→C has activation energy for the forward and the backward reaction has 25 kJ and 32 KJ respectively. The ΔH for the reaction is
View SolutionA reaction proceeds by first order, 75% of this reactin was completed in 32 min. The time required for 50% completion is
View SolutionRate expression for Xa+Yb→ products is Rate =K[A]m[B]n. Units of K w.r.t A and B respectively are s−1 and M−1s−1, when concentrations of A and B are increased by 4 times, then
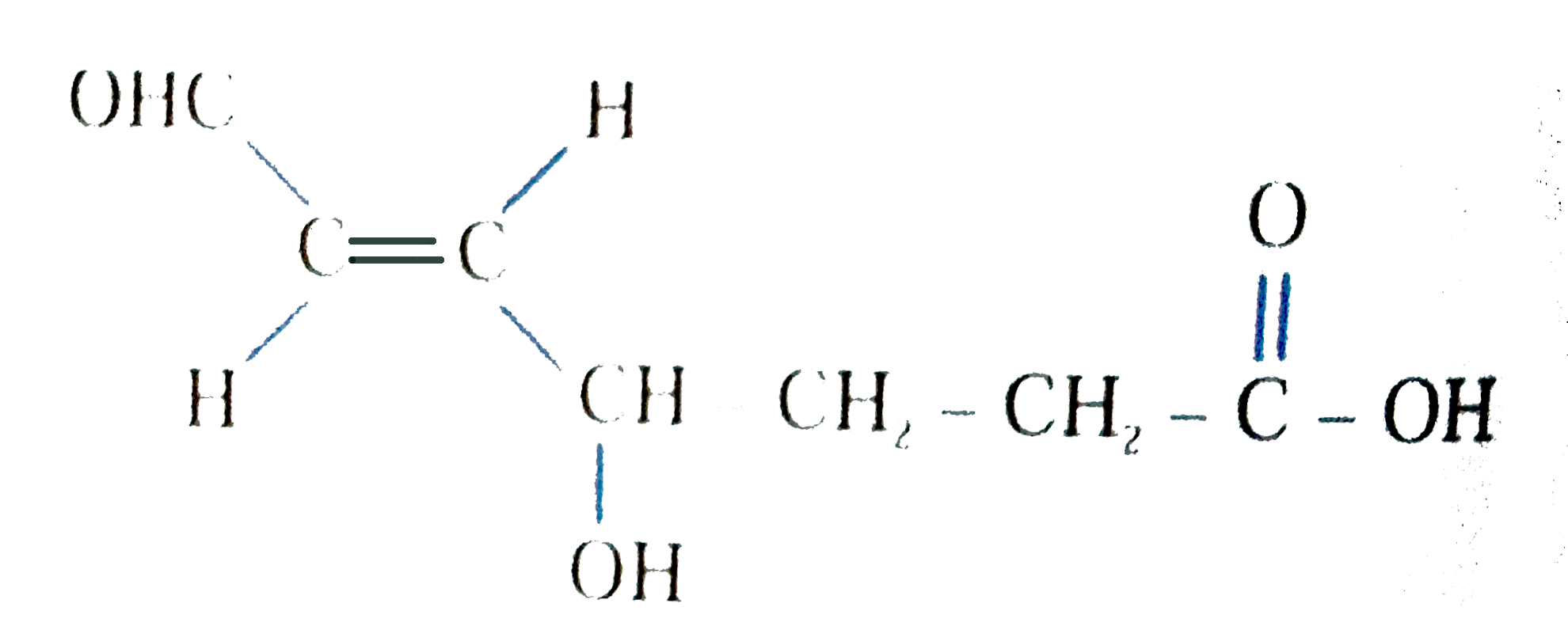
View SolutionProvide IUPAC name of the compound given below.
View Solution(A) Analgesics bring down body temperature during high fever.
(R ) Tetracyclin is a tranquillizer.
View Solution54.5mg of Na3po4 contains p32 (15.6% of sample) and P31 atoms. Assuming only P32 (15.6% of sample) and P31 atoms. Assuming only P32 atoms radioactive caculate the rate of decay for the given sample of Na3PO4 (Half-life period for p32=14.3 days mol. we of Na2PO4=161.2)
View SolutionThe half-life of the isotope ._11 Na^24 is 15 hrs. How much time does it take for (7)/(8) th of a sample of this isotope to decay ?
View SolutionThere are 4√2×106 radioactive nuclei in a given radioactive sample. If half life of sample is 20s, how many nuclei will decay in 10seconds?
View SolutionOne microgram of phosphorus-32 was injected into a live syetm for biological studies. The half life 15P32 is 14.3 days, calculate the time it will take the radioactivity to fall to 10% of the initial value
View SolutionState the law of radioactive decay. 3/4th of a radioactive sample decays in 3/4 s. What is the half-life of the sample?
View SolutionThe half-life of iodine-131 is 8.02 days. How long will it take for 80% of the sample to decay?
View Solutionकिसी रेडियोएक्टिव पदार्थ जिसकी अर्ध्दआयु 22 वर्ष है को क्षयित होकर 10% होने में कितना समय लगेगा ?
View SolutionA radioactive sample has half-life of 5 days. To decay from 8muCu to lmuCu , the number of days taken will be,
View SolutionHalf-life of a radioactive sample is 200 days. Its decay constant is
View SolutionA radioactive substance decays at 1/32 of its initial activity in 25 days. Its half life is :
View Solution

