Assertion (A) : Rate of reaction will be doubled, when temperature increased from 298 k to 308 k.
Reason (R ): The activation energy of reaction decreases with increase in temperature.
Both (A ) and (R) are true (R ) is the correct explanation to (A)
Both (A) and (R ) are true but (R) is not the correct explanation to (A)
(A)is true but (R) is false
Both (A) and (R) are false
The correct Answer is:C
To solve the given question, we need to analyze both the assertion (A) and the reason (R) provided.
Step 1: Analyze the Assertion (A)
The assertion states that the rate of reaction will be doubled when the temperature is increased from 298 K to 308 K.
- Explanation: It is a well-known principle in chemical kinetics that increasing the temperature generally increases the rate of reaction. This is primarily due to the increase in kinetic energy of the molecules, which leads to more frequent and effective collisions. Empirical observations suggest that for many reactions, a temperature increase of about 10 degrees Celsius (or 10 K) can approximately double the reaction rate.
Step 2: Analyze the Reason (R)
The reason states that the activation energy of the reaction decreases with an increase in temperature.
- Explanation: This statement is incorrect. The activation energy (Ea) is a characteristic of the reaction and does not change with temperature. While the number of molecules that have enough energy to overcome the activation barrier increases with temperature, the activation energy itself remains constant. The Arrhenius equation supports this, as it shows that the rate constant (k) depends on the activation energy and temperature, but not that the activation energy decreases with temperature.
Step 3: Conclusion
Based on the analysis:
- Assertion (A) is true.
- Reason (R) is false.
Therefore, the correct answer to the question is that A is true but R is false.
Final Answer
The correct answer is: C (A is true, R is false).
---
The assertion states that the rate of reaction will be doubled when the temperature is increased from 298 K to 308 K.
The reason states that the activation energy of the reaction decreases with an increase in temperature.
Based on the analysis:
- Assertion (A) is true.
- Reason (R) is false.
The correct answer is: C (A is true, R is false).
Topper's Solved these Questions
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:EXERCISE -1 (C.W) (ORDER OF REACTION)
Explore 14 Videos
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:EXERCISE -1 (C.W) (MOLECULARITY)
Explore 5 Videos
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:CUQ (RATE OF REACTION)
Explore 83 Videos
- CARBOXYLIC ACIDBook:NARAYNAChapter:CARBOXYLIC ACIDExercise:All Questions
Explore 288 Videos
- CHEMISTRY IN EVERYDAY LIFEBook:NARAYNAChapter:CHEMISTRY IN EVERYDAY LIFEExercise:ASSERTION & REASON TYPE QUESTIONS
Explore 10 Videos
Similar Questions
for a reaction 2A+3B→Products, the rate law expression is given by rate = K(A)1(B)2 . The order of the reaction with respect to A,B and over all order of reaction ar
View SolutionMolecularity of the following elementary reactions 2NO+O2→2NO2
View SolutionUnder a given set of experiemental condition, with increase in the concentration of the reactants, the reate of a chemical reaction
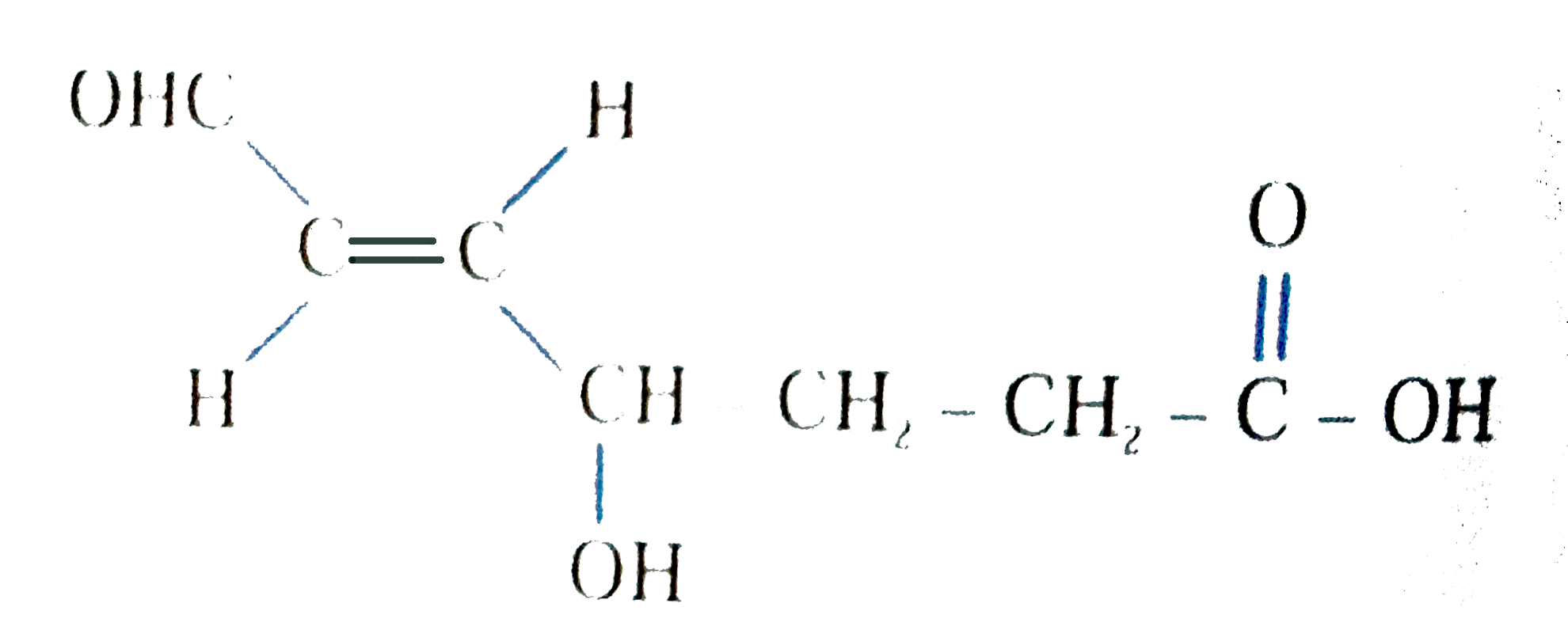
View SolutionProvide IUPAC name of the compound given below.
View Solution(A) Analgesics bring down body temperature during high fever.
(R ) Tetracyclin is a tranquillizer.
View SolutionAssertion (A) : The rate of a chemical reaction whether exothermic or endothermic increases with temperature. Reason (R ): The rate reaction =k[Reactant]n and k increases with temperature.
View SolutionThe activation energy of a reaction is 9.0 kcal//mol . The increase in the rate consatnt when its temperature is increased from 298 K to 308 K is
View SolutionThe rate of a reaction A doubles on increasing the temperature from 300 to 310 K. By how much, the temperature of reaction B should be increased from 300 K so that rate doubles if activation energy of the reaction B is twice to that of reaction A
View SolutionThe activation energy of a reaction is 9.0kcal/mol.
The increase in the rate consatnt when its temperature is increased from 298K to 308K is
View Solutionउस अभिक्रिया की सक्रियण ऊर्जा ज्ञात करो जिसका ताप 310 K से बढ़ाकर 320 K करने पर अभिक्रिया की दर दोगुनी हो जाती है
View SolutionThe rate constant of a reaction is doubled when the temperature is raised from 298 K to 308 K. Calculate the activation energy.
View Solutionपरम ताप , 298 K में 10 K की वृद्धि होने पर रासायनिक अभिक्रिया का वेग दुगुना हो जाता है । इस अभिक्रिया के लिये Eaकी गणना कीजिये ।
View SolutionThe rates of most reactions double when their temperature is raised from 298 K to 308 K. Calculate their activation energy.
View SolutionThe rate of most of reaction double when their temperature is raised from 298 K to 308 K. Calculate the activation energy of such a reaction.
View SolutionThe rate of most reactions becomes double when their temperature is raised from 298 K to 308 K. Calculate their activation energy.
View Solution