For a first order reaction, if ‘a’ is the initial concentration of reactant, then the half life time is
independent of a
∝a
∝a2
∝a3
The correct Answer is:A
To determine the half-life of a first-order reaction, we can follow these steps:
Step 1: Understand the concept of half-life
The half-life (t₁/₂) of a reaction is the time required for the concentration of a reactant to decrease to half of its initial concentration.
Step 2: Write the integrated rate law for a first-order reaction
For a first-order reaction, the integrated rate law can be expressed as:
ln((A)0(A))=kt
Where:
- (A)0 is the initial concentration of the reactant,
- (A) is the concentration at time t,
- k is the rate constant,
- t is the time.
Step 3: Set up the equation for half-life
At half-life, the concentration of the reactant will be half of the initial concentration:
(A)=(A)02
Substituting this into the integrated rate law gives:
ln⎛⎜⎝(A)0(A)02⎞⎟⎠=kt1/2
Step 4: Simplify the equation
This simplifies to:
ln(2)=kt1/2
Step 5: Solve for half-life
Rearranging the equation to solve for t1/2 gives:
t1/2=ln(2)k
Step 6: Substitute the value of ln(2)
The value of ln(2) is approximately 0.693. Therefore, we can express the half-life as:
t1/2=0.693k
Conclusion
The half-life of a first-order reaction is independent of the initial concentration and is given by the formula:
t1/2=0.693k
The half-life (t₁/₂) of a reaction is the time required for the concentration of a reactant to decrease to half of its initial concentration.
For a first-order reaction, the integrated rate law can be expressed as:
ln((A)0(A))=kt
Where:
- (A)0 is the initial concentration of the reactant,
- (A) is the concentration at time t,
- k is the rate constant,
- t is the time.
At half-life, the concentration of the reactant will be half of the initial concentration:
(A)=(A)02
ln⎛⎜⎝(A)0(A)02⎞⎟⎠=kt1/2
This simplifies to:
ln(2)=kt1/2
Rearranging the equation to solve for t1/2 gives:
t1/2=ln(2)k
The value of ln(2) is approximately 0.693. Therefore, we can express the half-life as:
t1/2=0.693k
The half-life of a first-order reaction is independent of the initial concentration and is given by the formula:
t1/2=0.693k
Topper's Solved these Questions
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:EXERCISE -1 (C.W) (RATE OF REACTION & FACTORS)
Explore 14 Videos
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:EXERCISE -1 (C.W) (ORDER OF REACTION)
Explore 14 Videos
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:CHECK YOUR GRASP
Explore 14 Videos
- CARBOXYLIC ACIDBook:NARAYNAChapter:CARBOXYLIC ACIDExercise:All Questions
Explore 288 Videos
- CHEMISTRY IN EVERYDAY LIFEBook:NARAYNAChapter:CHEMISTRY IN EVERYDAY LIFEExercise:ASSERTION & REASON TYPE QUESTIONS
Explore 10 Videos
Similar Questions
The rate of a gaseous reaction is given by the expression k [A] [B]. If the volume of the reaction vessel is suddenly reduced to 1/4th of the initial volume, the reaction rate relating to original rate will be
View Solutionfor a reaction 2A+3B→Products, the rate law expression is given by rate = K(A)1(B)2 . The order of the reaction with respect to A,B and over all order of reaction ar
View SolutionWhat is the instantaneous rate of a reaction.
View SolutionProvide IUPAC name of the compound given below.
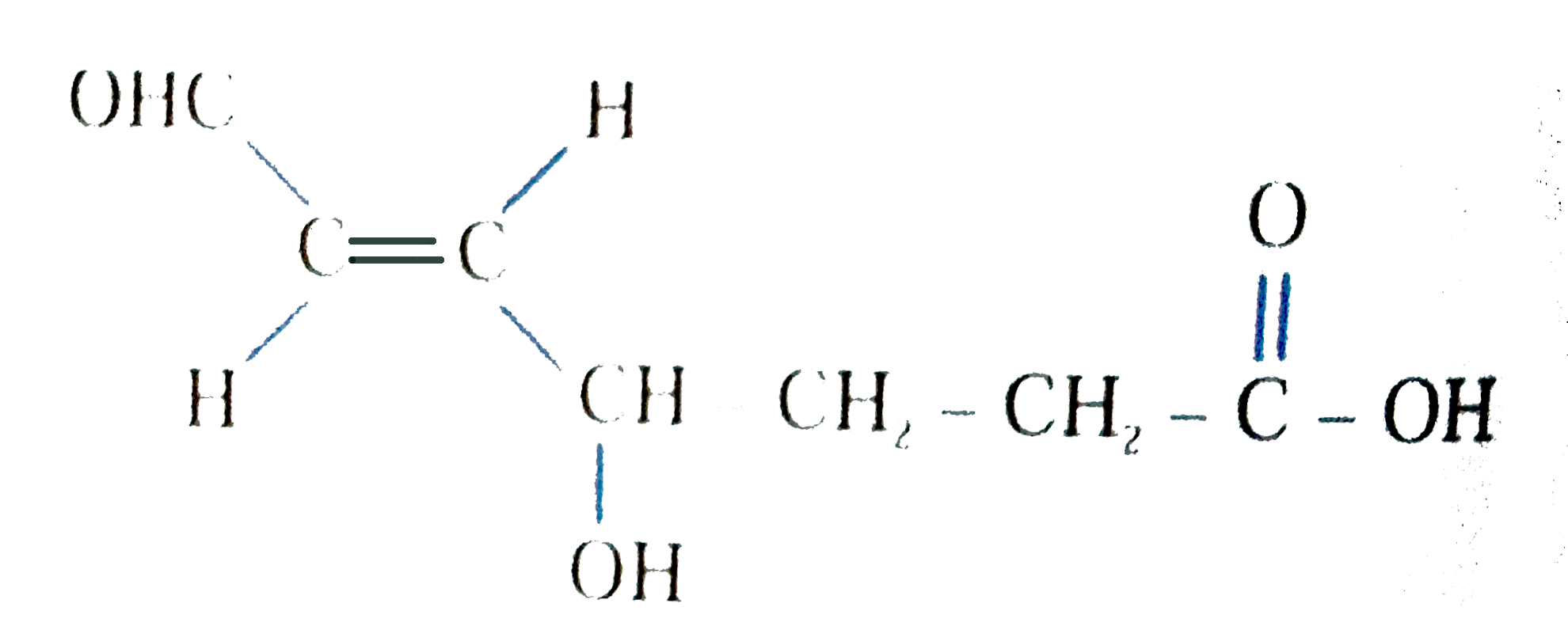
View Solution(A) Analgesics bring down body temperature during high fever.
(R ) Tetracyclin is a tranquillizer.
View SolutionFor the first order reaction half-life time is ………….. on the initial concentration.
View SolutionThe half-life of a first order reaction is 30 min and the initial concentration of the reactant is 0.1 M. If the initial concentration of reactant is doubled, then the half-life of the reaction will be
View Solutionसिद्ध कीजिए कि शून्य कोटि कि अभिक्रिया का अर्द्ध-आयुकाल अभिकारक की प्रारंभिक सान्द्रता के समानुपाती होता है।
View SolutionThe half life of a first order reaction is 30 min and the initial concentration of the reactant is 0.1 M . If the initial concentration of reactant is doubled ,then the half life of the reaction will be
View SolutionThe half-life of a reaction is halved as the initial concentration of the reaction is doubled. The order of the reaction is
View SolutionAssertion. Half-life of a reaction is independent of the initial concentration of the reactant. Reason. Half-life of a reaction is independent of the order of reaction.
View Solutionप्रथम कोटि की अभिक्रिया के लिए अर्ध आयु काल, अभिकारक की प्रारंभिक सांद्रता के……………….. होता है
View SolutionHalf life period of zero order reaction is ........... proportional to initial concentration of the reactant.
View SolutionShow that for the first order reaction half life is independent of initial concentration of reactant.
View SolutionShow that for a first order reaction, the half life is independed of the initial concentration of reactant.
View Solution

