In the reaction A+B⇒Products, if B is taken in excess, then it is an example of
Second order reaction
Zero order reaction
Fractional order reaction
First order reaction
The correct Answer is:D
To determine the order of the reaction A+B→Products when B is taken in excess, we can follow these steps:
1. Understanding the Reaction: The reaction involves two reactants, A and B, combining to form products. The stoichiometry of the reaction is 1:1.
2. Writing the Rate Law: The general form of the rate law for this reaction can be expressed as:
Rate=k(A)m(B)n
where k is the rate constant, and m and n are the orders of the reaction with respect to A and B, respectively.
3. Determining the Order: Since the stoichiometry of A and B is 1:1, we initially assume that m=1 and n=1. Therefore, the overall order of the reaction would be:
Overall Order=m+n=1+1=2
This indicates that the reaction is second order under normal conditions.
4. Considering B in Excess: When B is in excess, its concentration remains relatively constant during the reaction. This means that changes in the concentration of B will not significantly affect the rate of the reaction.
5. Revising the Rate Law: When B is in excess, we can simplify the rate law. The concentration of B can be treated as a constant, leading to a modified rate law:
Rate=k′(A)
where k′=k(B)n (with n being constant).
6. Determining the New Order: With B treated as a constant, the rate law now depends only on the concentration of A. This means the reaction behaves as a first-order reaction with respect to A:
Overall Order=1
7. Conclusion: Therefore, when B is taken in excess, the reaction A+B→Products behaves as a first-order reaction with respect to A.
Final Answer:
The reaction A+B→Products with B taken in excess is an example of a first-order reaction.
---
Rate=k(A)m(B)n
where k is the rate constant, and m and n are the orders of the reaction with respect to A and B, respectively.
Overall Order=m+n=1+1=2
This indicates that the reaction is second order under normal conditions.
Rate=k′(A)
where k′=k(B)n (with n being constant).
Overall Order=1
The reaction A+B→Products with B taken in excess is an example of a first-order reaction.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -1 (C.W) (RATE OF REACTION & FACTORS)14videos
CHEMICAL KINETICS
- BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - EXERCISE -1 (C.W) (ORDER OF REACTION)14videos
CHEMICAL KINETICS
- BOOK - NARAYNACHAPTER - CHEMICAL KINETICS EXERCISE - CHECK YOUR GRASP14videos
CHEMICAL KINETICS
- BOOK - NARAYNACHAPTER - CARBOXYLIC ACIDEXERCISE - All Questions288videos
CARBOXYLIC ACID
- BOOK - NARAYNACHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - ASSERTION & REASON TYPE QUESTIONS10videos
CHEMISTRY IN EVERYDAY LIFE
Similar Questions
Knowledge Check
- Question 1 - Select One
For a reaction A+B→ products, when B is taken in excess, then the rate law expression can be written as
ARate =K[A]1[B]0BRate =K[A]1[B]2CRate =K[A][B]DRate =K[A]2[B]1 - Question 2 - Select One
In the reaction
_S01_355_Q01.png)
the product (B) is:A_S01_355_O01.png)
B_S01_355_O02.png)
C_S01_355_O03.png)
D_S01_355_O04.png)
- Question 3 - Select One
For the reaction 2A + 3B → product, A is in excess and on changing the concentration of B from 0.1 M to 0.4 M, rate becomes doubled. Thus, rate law is :
Adxdt=k[A]2[B]2Bdxdt=k[A][B]Cdxdt=k[A]0[B]2Ddxdt=k[B]1/2
In the given reaction
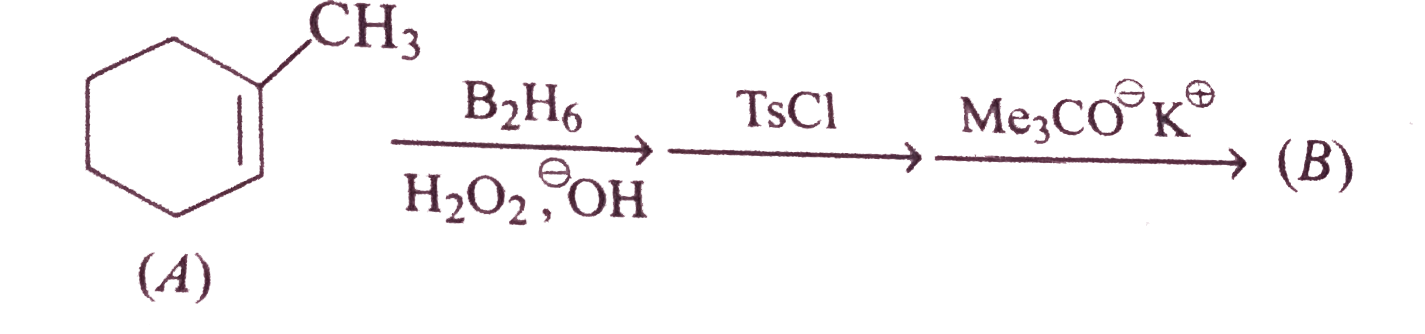
The product B is:View SolutionIn the given reaction :
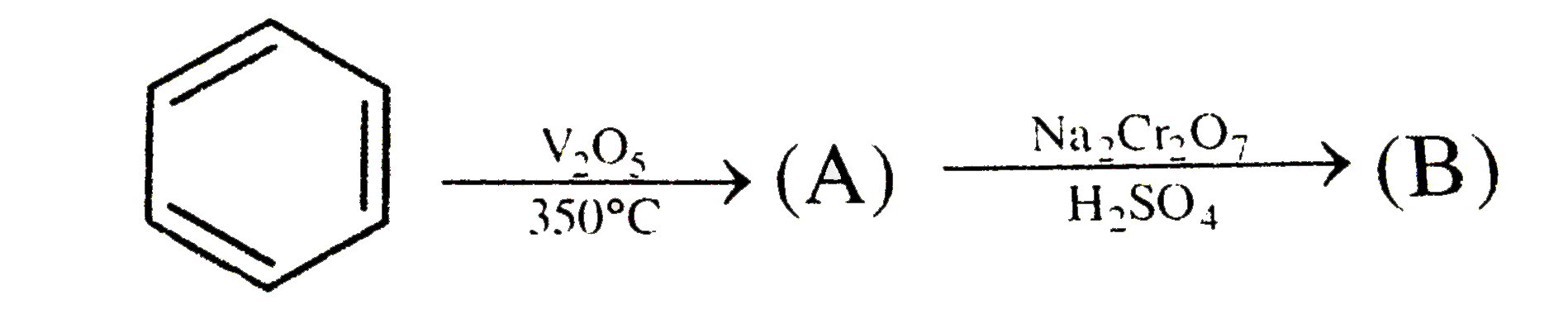
Product (B) is :View SolutionFor the reaction A+B products, it is observed that:
(1) on doubling the initial concentration of A only, the rate of reaction is also doubled and
(2) on doubling te initial concentration of both A and B, there is a charge by a factor of 8 in the rate of the reaction.
The rate of this reaction is given byView SolutionIn the reaction sequence
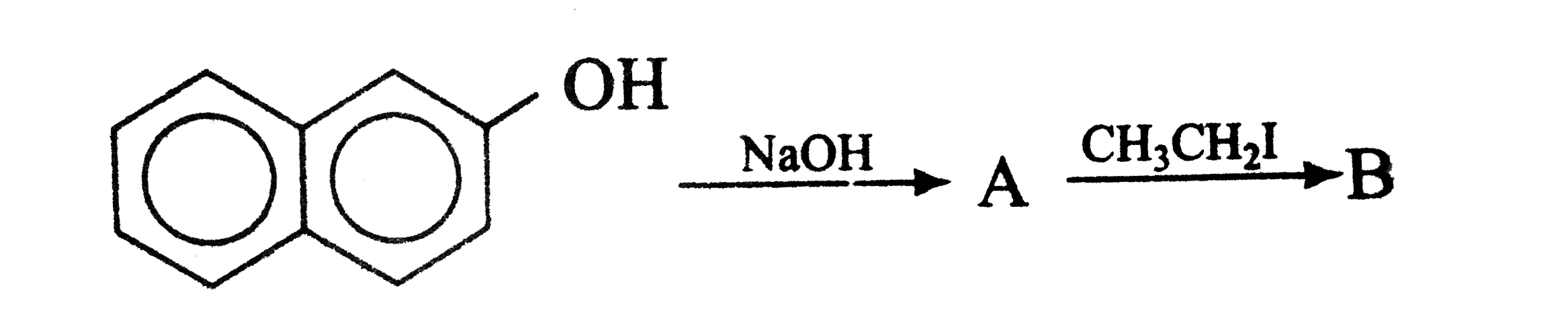
The product (B) isView SolutionIn the reaction
the product b isView Solution