An ideal gas will have maximum density when
P=0.5 atm , T = 600 K
P = 2 atm , T = 150 K
P = 1 atm , T = 300 K
P = 1.0 atm , T = 500 K
The correct Answer is:B
To determine when an ideal gas will have maximum density, we can follow these steps:
1. Understand the Ideal Gas Law:
The ideal gas law is given by the equation:
PV=nRT
where P is pressure, V is volume, n is the number of moles, R is the gas constant, and T is temperature.
2. Relate Density to the Ideal Gas Law:
We know that density (ρ) can be expressed as:
ρ=massvolume=n⋅MV
where M is the molar mass of the gas. Substituting n=PVRT into the density equation gives:
ρ=PMRT
3. Identify the Relationship Between Density, Pressure, and Temperature:
From the equation ρ=PMRT, we can see that:
ρ∝PT
This means that density is directly proportional to pressure and inversely proportional to temperature.
4. Maximize Density:
To maximize density, we need to maximize P (pressure) and minimize T (temperature). Therefore, the conditions for maximum density occur when pressure is at its highest and temperature is at its lowest.
5. Evaluate Given Options:
Suppose we have four options with different pressures and temperatures. We need to identify which option has the highest pressure and the lowest temperature:
- Option A: 0.5 atm, 300 K
- Option B: 2 atm, 150 K
- Option C: 1 atm, 250 K
- Option D: 1 atm, 350 K
In this case:
- Option B has the highest pressure (2 atm) and the lowest temperature (150 K).
6. Conclusion:
Since option B has the highest P and the lowest T, it will yield the maximum density. Therefore, the answer is:
Option B
The ideal gas law is given by the equation:
PV=nRT
where P is pressure, V is volume, n is the number of moles, R is the gas constant, and T is temperature.
We know that density (ρ) can be expressed as:
ρ=massvolume=n⋅MV
where M is the molar mass of the gas. Substituting n=PVRT into the density equation gives:
ρ=PMRT
From the equation ρ=PMRT, we can see that:
ρ∝PT
This means that density is directly proportional to pressure and inversely proportional to temperature.
To maximize density, we need to maximize P (pressure) and minimize T (temperature). Therefore, the conditions for maximum density occur when pressure is at its highest and temperature is at its lowest.
Suppose we have four options with different pressures and temperatures. We need to identify which option has the highest pressure and the lowest temperature:
- Option A: 0.5 atm, 300 K
- Option B: 2 atm, 150 K
- Option C: 1 atm, 250 K
- Option D: 1 atm, 350 K
- Option B has the highest pressure (2 atm) and the lowest temperature (150 K).
Since option B has the highest P and the lowest T, it will yield the maximum density. Therefore, the answer is:
Option B
Topper's Solved these Questions
- STATES OF MATTERBook:NARAYNAChapter:STATES OF MATTERExercise:EXERCISE - 2
Explore 42 Videos
- STATES OF MATTERBook:NARAYNAChapter:STATES OF MATTERExercise:EXERCISE - 3
Explore 32 Videos
- STATES OF MATTERBook:NARAYNAChapter:STATES OF MATTERExercise:CUQ
Explore 35 Videos
- SOME BASIC PRINCIPLES AND TECHNIQUESBook:NARAYNAChapter:SOME BASIC PRINCIPLES AND TECHNIQUESExercise:EXERCISE -IV (QUALITATIVE AND QUANTITATIVE ANALYSIS OF ORGANIC OF COMPOUNDS)
Explore 8 Videos
- STRUCTURE OF ATOMBook:NARAYNAChapter:STRUCTURE OF ATOMExercise:EXERCISE - IV EXEMPLAR PROBLEMS
Explore 24 Videos
Similar Questions
An ideal gas 'X' has same density at 1 bar pressure as that of dinitrogen at 2 bar at 298 K. What is the molar mass of the gas 'X'?
View SolutionAn ideal gas with the adiabatic exponent γ goes through a process p=p0−αV, where p0 and α are positive constants, and V is the volume. At what volume will the gas entropy have the maximum value ?
View Solution
Knowledge Check
An ideal gas will have maximum density when
AP=0.5atm,T=600KBP=2 at, T =150KCP=1 atm, T=300KDP=1.0 atm, T=500KWhich of the following samples of ideal gas will have maximum translation kinetic energy??
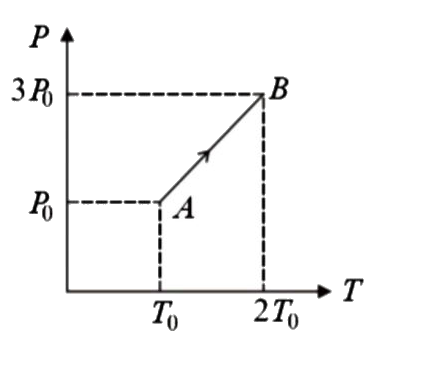
A12 mole of CO(g) at 400KB16g of oxygen gas at 200KC28g of nitrogen gas at 300KD1g of ozone at 600KPressure versus temperature graph of an ideal gas is shown in figure. Density of the gas at point A is P0. Density at B will be
 A34ρ0B32ρ0C43ρ0D2ρ0
A34ρ0B32ρ0C43ρ0D2ρ0
An ideal gas with density of 3.0 g/L has pressure of 675 mmHg at 25∘C . What is the rms speed of the molecules of this gas?
View SolutionIf P, V, M, T and R are symbols of pressure, volume, molecular weight, temperature and Gas contstant, what is the equation of density of ideal gas
View SolutionA vander Waals' gas may behave ideally when
View SolutionPressure versus temperature graph of an ideal gas is as shown in figure. Density of the gas at point A is ρ0. Density at point B will be :-
View SolutionThe work done by a gas is maximum when it expands
View Solution