Which of the following curves may represent the radius of orbit (rn) in a H-atoms as a function of principal quantum number(n)
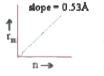

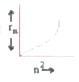
None of these
The correct Answer is:B
To determine which curve represents the radius of orbit rn in a hydrogen atom as a function of the principal quantum number n, we can follow these steps:
1. Understand the Formula: According to Bohr's model of the hydrogen atom, the radius of the nth orbit is given by the formula:
rn=0.529n2Z angstroms
For hydrogen, Z=1, so the formula simplifies to:
rn=0.529n2 angstroms
2. Identify the Relationship: The relationship between the radius rn and the principal quantum number n is quadratic, meaning that rn is proportional to n2. This indicates that if we plot rn on the y-axis and n on the x-axis, the graph will be a parabola.
3. Analyze the Options:
- Option 1: If rn is plotted against n, it will not be a straight line but a curve (parabola), which is incorrect.
- Option 2: If rn is plotted against n2, we can express it as:
rn=0.529×n2
Here, if we let n2 be on the x-axis and rn on the y-axis, this is a linear relationship of the form y=mx where m=0.529. This is a straight line, which is correct.
- Option 3: This option suggests a graph that starts as a straight line and then curves, which is incorrect because the relationship is purely linear when plotted against n2.
- Option 4: This option states "none of these," which is also incorrect since we have identified Option 2 as correct.
4. Conclusion: The correct option that represents the radius of orbit rn in hydrogen atoms as a function of the principal quantum number n is Option 2.
rn=0.529n2Z angstroms
For hydrogen, Z=1, so the formula simplifies to:
rn=0.529n2 angstroms
- Option 1: If rn is plotted against n, it will not be a straight line but a curve (parabola), which is incorrect.
- Option 2: If rn is plotted against n2, we can express it as:
rn=0.529×n2
Here, if we let n2 be on the x-axis and rn on the y-axis, this is a linear relationship of the form y=mx where m=0.529. This is a straight line, which is correct.
- Option 3: This option suggests a graph that starts as a straight line and then curves, which is incorrect because the relationship is purely linear when plotted against n2.
- Option 4: This option states "none of these," which is also incorrect since we have identified Option 2 as correct.
Topper's Solved these Questions
- STRUCTURE OF ATOMBook:NARAYNAChapter:STRUCTURE OF ATOMExercise:EXERCISE - I (H. W.) dE-BROGLIE.S & HEISENBERG.S
Explore 2 Videos
- STRUCTURE OF ATOMBook:NARAYNAChapter:STRUCTURE OF ATOMExercise:EXERCISE - I (H. W.) QUANTUM MECHANICAL MODEL OF ATOM
Explore 6 Videos
- STRUCTURE OF ATOMBook:NARAYNAChapter:STRUCTURE OF ATOMExercise:EXERCISE - I (H. W.) H-SPECTRUM
Explore 5 Videos
- STATES OF MATTERBook:NARAYNAChapter:STATES OF MATTERExercise:A & R TYPE QUESTIONS
Explore 16 Videos
- THERMODYNAMICSBook:NARAYNAChapter:THERMODYNAMICSExercise:Assertion- Reason
Explore 5 Videos
Similar Questions
Which ofthe following curves may represent the energy of electron in hydrogen atom as a function of principal quantum number n:
View SolutionWhich of the plots shown in the figure represents speed (vn) of the electron in a hydrogen atom as a function of the principal quantum number (n)?
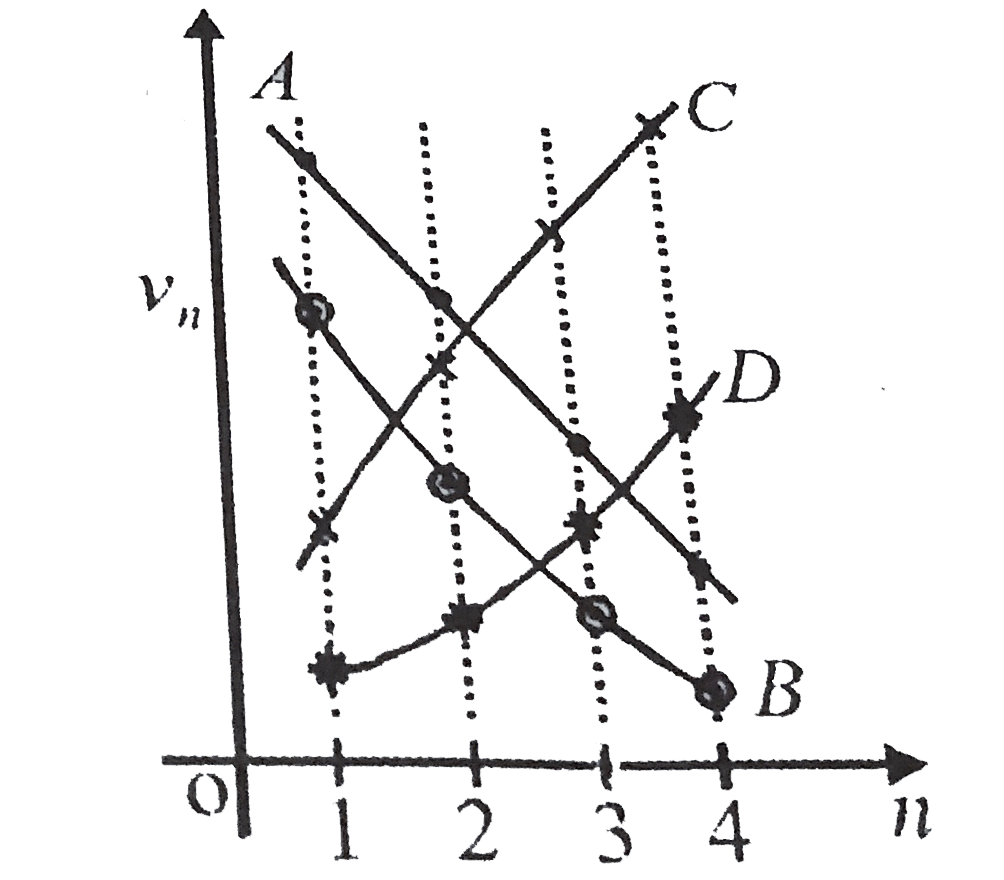
View Solution
Knowledge Check
Which of the following curves may represent the radius of orbit (rn) in H-atoms as a function of principal quantum number (n)
A B
B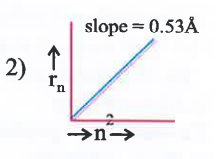 C
C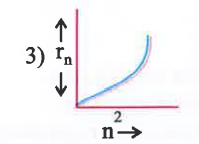 DNone of these
DNone of theseWhich of the following curves may represent the speed of the electron in a hydrogen atom as a function of the principal quantum number n ?
A B
B C
C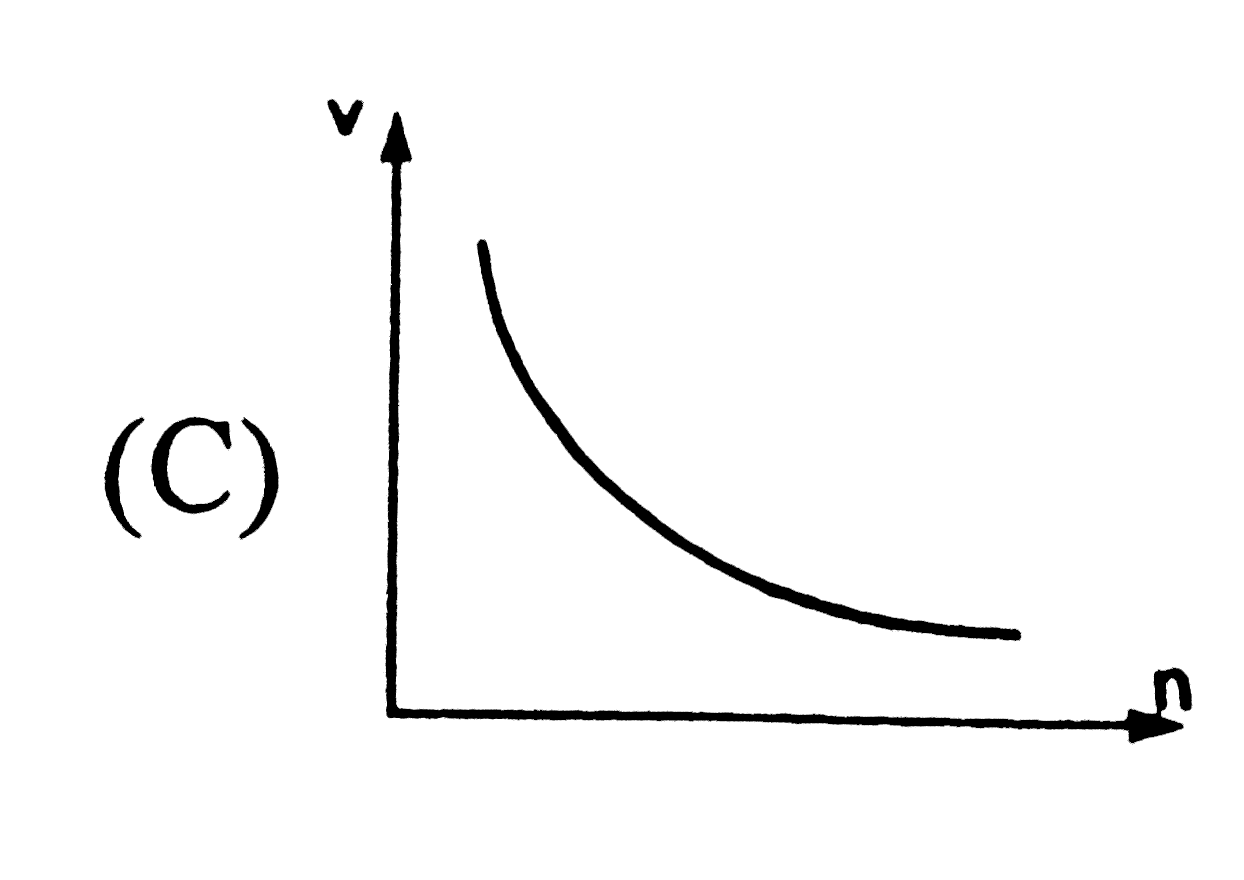 D
D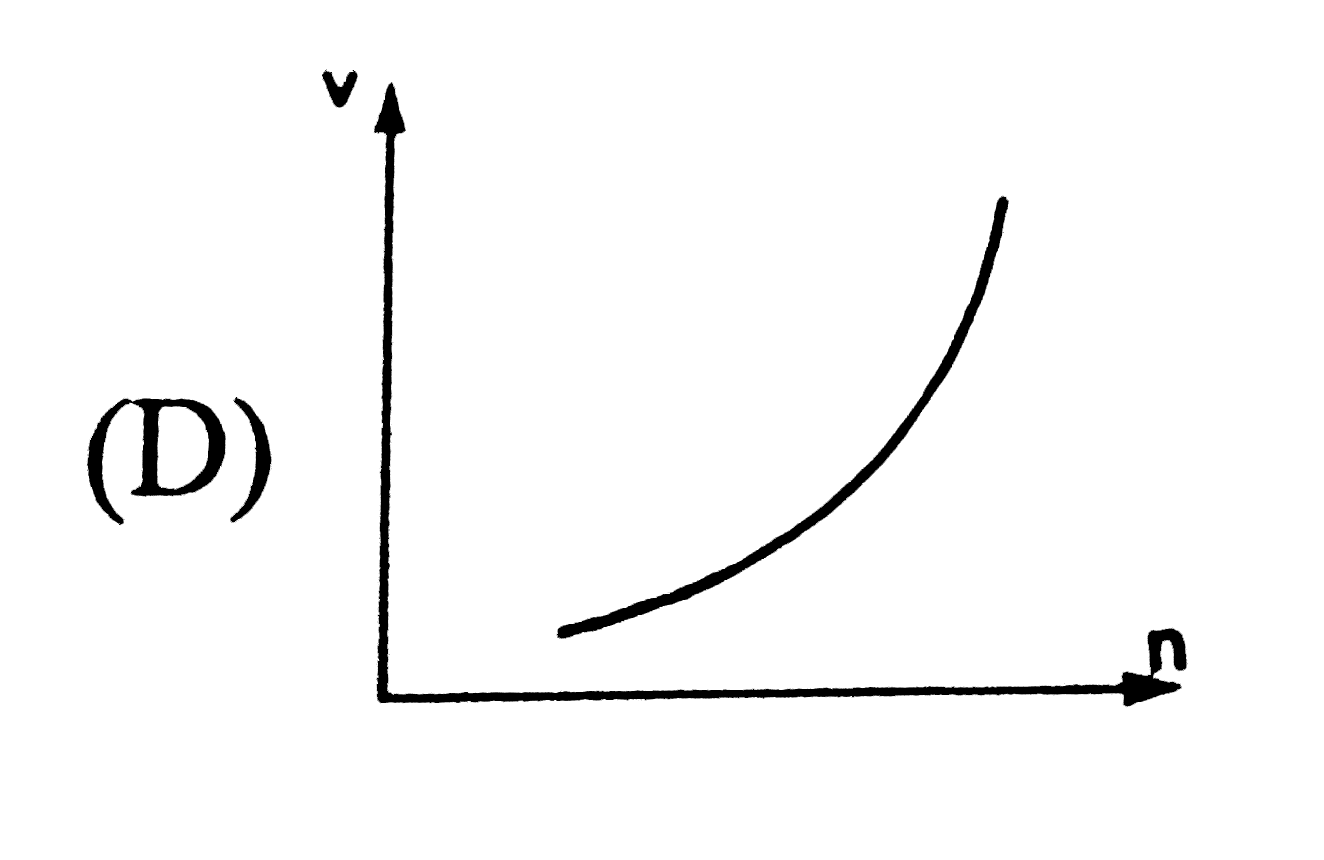
The principal quantum number represent
AShape of an orbitalBDistance of electron from nucleusCNumber of electrons in an orbitDNumber of orbitals in an orbit
Which of the following expressions represents the spectrum of Balmer series (If n is the principal quantum number of higher energy level) in Hydrogen atom ?
View SolutionShow that the radius of the orbit in hydrogen atom varies as n2, where n is the principal quantum number of the atom.
View SolutionThe principal quantum number, n describes
View SolutionFor a shell of principal quantum number n=4, there are:
View Solutionwhat is the total number of orbitals associated with the principal quartum number n= 3?
View Solution