If x, y, z are in arithmetic progression and a is the arithmetic mean of x and y and b is the arithmetic mean of y and z, then prove that y is the arithmetic mean of a and b.
A
x=y<z
B
x=y>z
C
x<z<y
D
x>z<y
Video Solution
Text Solution
The correct Answer is:C
x=a+b=14±0.14⇒%error =0.1414×100=1%,y=a−b=2±0.14⇒% error =0.142×100=7%
z=ab=48±0.96⇒% error =0.9648×100=2%. Therefore order of % error is x<z<y
|
Topper's Solved these Questions
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:BEGINNER S BOX-1
Explore 2 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:BEGINNER S BOX-2
Explore 4 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:SUBJECTIVE QUESTION
Explore 9 Videos
- SEMICONDUCTORSBook:ALLENChapter:SEMICONDUCTORSExercise:Part-3(Exercise-4)
Explore 51 Videos
Similar Questions
Ifx,y,z are in A.P. andA1is the arithmetic mean of x,y and A2is the arithmetic mean of y,z then prove that the arithmetic mean of A1and A2isy
View SolutionIf ‘a', is the Arithmetic mean of b and c, 'b', is the Geometric mean of c and a, then prove that 'c' is the Harmonic mean of a and b.
View Solution
Knowledge Check
Find the arithmetic mean of:
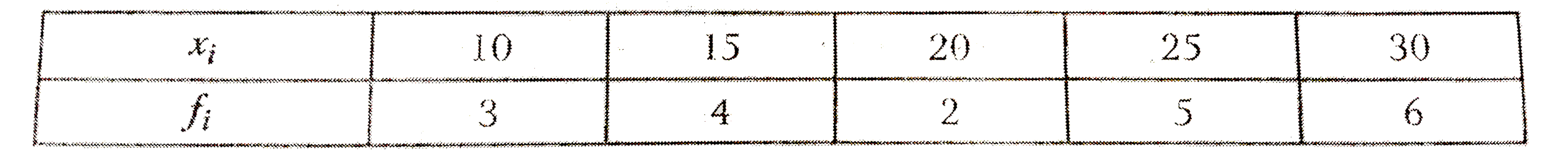 A21B21.4C22.75D21.75
A21B21.4C22.75D21.75Find the arithmetic mean of 4 and 12.
A9B8C16D10The arithmetic mean between 8 and 12 is-
A9B10C4D6